CASYS'03
Sixth International Conference on
Computing Anticipatory Systems
Liege, Belgia, Sierpień 11-16, 2003
Streszczenie. Lingwistyczna relacja podmiot-przedmiot jest najbardziej istotnym kluczem w rozumieniu funkcjonowania przyrody, ponieważ jest ona bardzo ściśle związana z ludzkim umysłem oraz jest zawsze używana w każdym modelowaniu nawet, kiedy nie jesteśmy tego świadomi. Praca ta przedstawia nowe spojrzenie na elementarne i syntetyczne modele relacji podmiot-przedmiot, która zespala wszystkie dziedziny nauki. Spojrzenie to jest szczególnie korzystne dla fizyki i nauk społecznych, co jest zilustrowane przez przykłady zaczerpnięte z tych dziedzin. Pierwszy przykład zawiera nową interpretację zasady równoważności masy i energii, zasady nieoznaczoności oraz dualność materii. Drugi przykład jest nową fizyczną interpretacją procesów demokratycznych, która jest bardziej precyzyjna od powszechnie obowiązującej, gdyż bazuje na rzeczywistej istocie demokracji, a nie na sposobie jej realizacji. Pracę tę można zakwalifikować między innymi jako analizę wybranych szczegółowych związków języka z metodologią nauk.
1. Wprowadzenie
Rola języka w naukach jest bardzo ważna, gdyż z godnie z Wittgenstein'em język, myśl i rzeczywistość tworzą złożone związki (Wittgenstein LJ, 1961). Klucz do tych związków zawiera struktura zdania warunkowego, ponieważ jest ona najbardziej ważnym i uniwersalnym modelem każdego zjawiska i systemu (Turkiewicz K and Turkiewicz DB, 2002). Centralnym elementem tej struktury jest zdanie oznajmujące, zawierające relację podmiot-przedmiot która określa elementarny i syntetyczny sposób realizację wszystkich aktywności i zmian w przyrodzie. Relacja podmiot-przedmiot istnieje między wszystkimi elementami, systemami i zjawiskami. Tworzy ona nieograniczony zbiór relacji, które różnią się w sposób stopniowy od bardzo sztywnych i niszczących aż do elastycznych i całkowicie niezależnych. Pod pojęciem 'sztywność' rozumiemy cechę systemu albo procesu, która determinuje następujące ich zachowanie: im system lub proces jest sztywniejszy, tym trudniej jest zmienić ich charakterystyki.
Cecha sztywności systemów i procesów jest bardzo ważną charakterystyką, gdyż determinuje ich zdolności dokonywania zmian. Z jednej strony, sztywność wpływa na zachowywanie indywidualnych cech systemów i z drugiej strony ona ogranicza ich adaptację do zewnętrznych i wewnętrznych zmian. Znajomość i rozumienie tej cechy jest istotna, gdyż pozwalają one na zastosowanie efektywnego antycypacyjnego sterowania systemami, które wymaga wcześniejszego przygotowania odpowiednich sposobów i środków.
Obserwacje
różnych zjawisk przede wszystkim rejestrują zmiany wartości parametrów tych
zdarzeń w określonym przedziale czasu. W rezultacie takich obserwacji zauważamy,
że zmiany parametrów mogą być monotonicznymi lub cyklicznymi procesami
wzrostu i zmniejszania, które skrótowo nazywamy procesami wzrostu lub
wzrostem. Matematycznie wzrost jest określany przez dowolną teoretyczną, jak i empiryczną funkcję q(t) zmian 'q' w stosunku do czasu 't'.
Podstawowym bardzo ważnym parametrem wzrostu jest stosunek wyrażony przez
przyrosty Dq, Dt oraz dq i dt
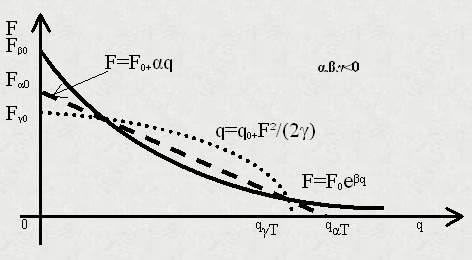
dla dq/dt=limDq/Dt dla
Dt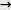 0. W fizyce funkcja q(t) jest nazywana intensywnością zmian albo intensywnością
działania siły, jeżeli 'q' reprezentuje siłę 'F'. Przykładowo
v=dx/dt jest intensywnością zmian dystansu 'x', i jest nazywane prędkością.
Natomiast intensywność p=dF/ds jest nazywane ciśnieniem, gdzie 'F' jest siłą,
a 's' powierzchnią na którą działa siła (Sussman GJ et al, 2001).
Jednak, taka metoda modelowania procesów bazująca na czasie, nie identyfikuje
przyczynowości zmian, ponieważ czas jest abstrakcyjnym elementem syntetyzującym
wszystkie zmiany i istnieje tylko w połączeniu z ludzkim umysłem. Ten aspekt
pojęcia czasu pokazują nasze analizy struktury zdania warunkowego (Turkiewicz
K and Turkiewicz DB, 2002).
0. W fizyce funkcja q(t) jest nazywana intensywnością zmian albo intensywnością
działania siły, jeżeli 'q' reprezentuje siłę 'F'. Przykładowo
v=dx/dt jest intensywnością zmian dystansu 'x', i jest nazywane prędkością.
Natomiast intensywność p=dF/ds jest nazywane ciśnieniem, gdzie 'F' jest siłą,
a 's' powierzchnią na którą działa siła (Sussman GJ et al, 2001).
Jednak, taka metoda modelowania procesów bazująca na czasie, nie identyfikuje
przyczynowości zmian, ponieważ czas jest abstrakcyjnym elementem syntetyzującym
wszystkie zmiany i istnieje tylko w połączeniu z ludzkim umysłem. Ten aspekt
pojęcia czasu pokazują nasze analizy struktury zdania warunkowego (Turkiewicz
K and Turkiewicz DB, 2002).
Zakładając, że abstrakcyjne pojęcie siła 'F' jest modelem dowolnego systemu posiadającego podmiotowe cechy, które powodują zmiany 'q' parametru 'p' drugiego systemu mającego cechy przedmiotowe, to możemy dla ciągłego procesu zdefiniować sztywność (wytrzymałość) drugiego systemu na działanie siły 'F' jako wyrażenie IRF=dqp, gdzie dF/dqp jest pochodną funkcji F(dqp). Z drugiej strony wyrażenie IRq=dqp/dF określa sztywność albo stałość (intensywność) procesu zmian 'qp'. Kiedy sztywność systemu IRF=dF/dqp jest odpowiednio duża lub IRq=dqp/dF jest mała, uważamy, że taki system jest względnie stałym obiektem albo cząstką. Kiedy IRF=dF/dqp jest odpowiednio mała lub IRq=dqp/dF jest odpowiednio duża, to taki system jest procesem albo przepływem. Natomiast, kiedy sztywność jest równa zeru, to siła 'F' i zmiana 'q' są niezależne względem siebie. Należy tu zaznaczyć, że parametry 'F' i 'q' reprezentują ilościowe miary sił i zmian, i dlatego generalnie, sztywność może być określana przez stosunek dowolnych dwóch parametrów, jak na przykład: siła, energia, moc, odległość, masa, prędkość i inne.
W rzeczywistości wszystkie złożone systemy oddziałują na drugie systemy albo otoczenia przy pomocy różnego rodzaju sił, które zmieniają ich odpowiednie parametry. Dlatego każdy system może charakteryzować się inną sztywnością dla poszczególnych jego parametrów. Ponieważ praca analizuje tylko główną ideę sztywności, dlatego nasze analizy są ograniczone do ciągłych funkcji F(q) dla jedno-wymiarowej przestrzeni (p=1).
Zaprezentowana matematyczna definicja sztywności relacji podmiot-przedmiot jest podstawą następującej interpretacji dualności w funkcjonowaniu przyrody na każdym poziomie jej struktury, która jest wynikiem z jednej strony wytrzymałością względnie stałych obiektów wyrażoną sztywnością dF/dq i z drugiej strony przez stałość zmian albo procesów wyrażoną sztywnością dq/dF. W tym ostatnim wyrażeniu 'q' jest modelem zmian, które pełnią funkcję albo rolę podmiotu w stosunku do siły 'F'. W ekstremalnym przypadku, kiedy szybkość zmian systemu jest odpowiednio bliska zeru, to nie jesteśmy w stanie zaobserwować tych zmian, i uważamy ten system za trwały. W przeciwnym ekstremalnym przypadku, kiedy element albo system zmienia lub porusza się z prędkością światła w próżni 'c', to nie jesteśmy w stanie zaobserwować cech trwałości stałych obiektów. Natomiast obserwujemy tylko stałe ciągłe zmiany. Ponieważ pojęcie energia określa zdolność dokonywania zmian, dlatego jest to również interpretacja zasady równoważności masy i energii. Interpretacja ta jest bardzo prosta w porównaniu do interpretacji, która wprowadza dodatkowy nieznany wymiar materii.
W kontekście języka, wszystkie obiekty, zmiany, jak i ich cechy są modelowane przy pomocy stałych informatycznych obiektów w postaci wyrazów (słów). Ponieważ język jest ściśle związany z każdą metodą modelowania, dlatego nie jest niezwykłym, że skrócone i/albo nielogicznie przyporządkowane materialne cechy są przypisane do informacyjnych obiektów i/lub informacyjne cechy do materialnych obiektów. Przykładowo, zwykle rozumiemy, że energia jest jakimś specyficznym materialnym fluidem i niektórzy fizycy uważają, że atomowe cząstki są wibracjami 'czystej energii', a przecież tylko jest pewne, że energia jest informacyjną ekstensywną charakterystyką relacji podmiot-przedmiot albo specyficzną (informacyjną) miarą aktywności materii, systemów i procesów. W bardzo wielu przypadkach zaprezentowane interakcje pomiędzy informacyjnymi modelami i rzeczywistością nie mają dużego wpływu na jakość modelowania, ale w przypadku dualności materii doprowadziły one do mistycznego wniosku, że istnieje dodatkowy nieznany wymiar materii.
Jeżeli materia zmienia się lub porusza z prędkością światła 'c', to proces ten nie może być opisany przy pomocy cech należących do względnie stałych materialnych obiektów. Jednak w modelowaniu, ten idealny ciągły proces opisujemy przy pomocy cech stałych informacyjnych obiektów, które mogą dotyczyć materialnych stałych obiektów lub zmiennych procesów. W związku z tym w obserwacjach cząstek atomowych poruszających się z prędkością blisko prędkości światła, które dokonuje się tylko w sposób pośredni przy pomocy modeli, zauważamy, że wyniki tych obserwacji odzwierciedlają typ użytego modelu, który ogólnie może być albo ciągły, albo dyskretny. Również, zależnie on ich prędkości, cząstki będą się bardziej charakteryzowały cechami stałych obiektów materialnych, im ich prędkość jest bardziej mniejsza od 'c' oraz w przeciwnym przypadku — bardziej cechami ciągłych procesów. Ponieważ cząstek atomowych nie można opisać przy pomocy parametrów używanych w modelowaniu względnie stałych obiektów, dlatego rozwinięto wizualne metody prawdopodobnych schematów trajektorii cząstek. (Liboff RL, 2003). Schematy te odzwierciedlają ograniczone obszary ruchu cząstek. Istota tych ograniczonych obszarów jest prezentowana w sekcji 3.
Ponieważ na funkcjonowanie ludzkiego umysłu silnie wpływa język charakteryzujący się dyskretną strukturą, dlatego modelowanie idealnie ciągłych lub bliskich nim procesów natrafia na duże trudności. Ten silny wpływ powoduje, że nauki nie mogą uciec czy pominąć szukania fundamentalnej językowej relacji albo korelacji podmiot-przedmiot. Przykładowo z tego względu w fizyce poszukuje się i bada cząstki materii, których czas trwania jest bardzo krótki.
2. Elementarne monotoniczne i ciągłe funkcje sztywności systemów
Fizycznie sztywność
relacji podmiot-przedmiot, zdefiniowaną jako pochodne funkcji F(q) i q(F), zależy
od własności systemu, którą syntetycznie nazywamy oporem lub siłą oporu.
Ponieważ siła ta nie tylko działa przeciwko zmianom, ale również dokonuje
zmiany, dlatego ma ona taka samą abstrakcyjną naturę jak pozytywnie lub
negatywnie działająca siła 'F', i dlatego może ona być pominięta nie
zmniejszając jakości modelowania. Jednak użycie terminu siła oporu może być
bardzo korzystne w modelowaniu i interpretacji modeli. W tym kontekście można
wyróżnić następujące trzy typy sztywności systemów i procesów:
1. stała i/lub niezależna od wielkości działających sił i/lub zmian,
2. zmienna proporcjonalnie do wielkości działających sił i/lub zmian,
3. zmienna odwrotnie proporcjonalnie wielkości działających sił i/lub.
Te rodzaje sztywności mogą być wyrażone w postaci następujących
monotonicznych funkcji albo różniczkowych równań pierwszego rzędu:
1.
IRa=dF/dq=a,
2. IRb=dF/dq=bF
lub IRb=dF/dq=bq,
3. IRg=dF/dq=g/F
lub IRg=dF/dq=g/q,
gdzie a, b i
g są stałymi współczynnikami,
których wartości są liczbami rzeczywistymi. Siła 'F' i zmiana 'q'
reprezentują odpowiednio podmiot lub przedmiot w relacji podmiot-przedmiot w zależności od względnej ich aktywności i/lub wartości sztywności. W dalszych analizach będziemy używać następujące funkcje otrzymane w wyniku
scałkowania tych wyrażeń:
1. F=F0 aq,
aq,
2. F=F0e bq lub
q=q0
bq lub
q=q0 lnF lub
F=F0
lnF lub
F=F0 bq2/2,
bq2/2,
3. F= (F0
(F0 2gq) lub
F=F0
2gq) lub
F=F0
 (2gq) lub
q=q0
(2gq) lub
q=q0 F2/(2g)
lub F=F0
F2/(2g)
lub F=F0 glnq
lub q=q0e
glnq
lub q=q0e F/g.
F/g.
W zależności od typu zjawiska, te podstawowe monotoniczne i ciągłe relacje podmiot-przedmiot możemy różnie interpretować, jak na przykład: użycie siły do dokonania zmian, dokonanie zmian w celu utworzenia siły itd. Dodatkowo, pozytywne i negatywne wartości zmian i sił mogą ściśle korelować z popularną miarą albo oceną społecznych zdarzeń i zjawisk, która używa skalę 'dobrze i źle' albo 'tak i nie'.
Oprócz funkcji F(q), q(F) i sztywności bardzo ważną cechą relacji
podmiot-przedmiot jest energia. Syntetycznym i elementarnym modelem tej własności
są następujące wyrażenia E=W=F q i dE=dW=dFdq, gdzie przestrzeń wektorów 'F'
i 'q' jest wielowymiarowa, a przestrzeń parametrów
'F' and 'q' jest jednowymiarowa. Dlatego, energia jako parametr
relacji podmiot-przedmiot jest E=óódFdq,
gdzie 'F' i 'q' należą do przedziałów określonych przez odpowiednie
ograniczenia F1, F2 i q1, q2.
Przykładowo dla relacji podmiot-przedmiot charakteryzującej się sztywnością
dF/dq=a, jej energia wynosi E=E0+aq2/2 lub E=E0+F2/2a (Sussman GJ et
al, 2001), natomiast dla sztywności dF/dq=g/q, jej energia E=E0+q(C+ln|q|).
Również pęd dp=dmdv jest charakterystyką podobną do energii lub może być
traktowany jako jej specyficznie zredukowana forma. W kontekście tej analizy możemy
powiedzieć, że energia jest ekstensywną, a sztywność — intensywną
informacyjną charakterystyką relacji podmiot-przedmiot.
q i dE=dW=dFdq, gdzie przestrzeń wektorów 'F'
i 'q' jest wielowymiarowa, a przestrzeń parametrów
'F' and 'q' jest jednowymiarowa. Dlatego, energia jako parametr
relacji podmiot-przedmiot jest E=óódFdq,
gdzie 'F' i 'q' należą do przedziałów określonych przez odpowiednie
ograniczenia F1, F2 i q1, q2.
Przykładowo dla relacji podmiot-przedmiot charakteryzującej się sztywnością
dF/dq=a, jej energia wynosi E=E0+aq2/2 lub E=E0+F2/2a (Sussman GJ et
al, 2001), natomiast dla sztywności dF/dq=g/q, jej energia E=E0+q(C+ln|q|).
Również pęd dp=dmdv jest charakterystyką podobną do energii lub może być
traktowany jako jej specyficznie zredukowana forma. W kontekście tej analizy możemy
powiedzieć, że energia jest ekstensywną, a sztywność — intensywną
informacyjną charakterystyką relacji podmiot-przedmiot.
Zaprezentowane monotoniczne funkcje sztywności mogą być podzielone na dwa rodzaje. Pierwszy rodzaj charakteryzuje się ujemnymi wartościami stałych a, b i g, natomiast drugi typ — dodatnimi wartościami tych współczynników. Rysunek 1. ilustruje podstawowe charakterystyki (funkcje) systemów F=f(q), których współczynniki a, b i g są negatywne (a,b,g<0). Takie systemy korespondują z systemami, których charakterystyki q=f(F) mają współczynniki dodatnie (a,b,g >0). Systemy takie mają zdolność łatwego dokonywania zmian, ponieważ ich opory przeciwko zmianom maleją wraz z ich realizacją. Dlatego systemy te nazywamy procesami lub przepływami. Rozważając procesy w kontekście pozytywno-negatywnej oceny, negatywne zmiany tworzą samoniszczące się procesy, jak na przykład starzenie i degradacja. Natomiast, dla pozytywnych zmian systemy takie ułatwiają procesy pozytywnego wzrostu. Dodatkową ważną cechą tych procesów jest to, że wraz z ich rozwojem po inicjacji, wewnętrzne ciśnienie systemu się zmniejsza. Paliwo jest typowym tego przykładem. Ogólnie jest akceptowane, że paliwo posiada odpowiednio dużą gęstość energii, która spontaniczne się wyzwala po inicjacji procesu jej wyzwalania (spalania). Szczególnym przykładem jest spontaniczna dezintegracja radioaktywnych izotopów wyrażana funkcją N=N0e-lt, której struktura jest identyczna z funkcją F=F0e-bq (Liboff RL, 2003). W ekonomii funkcje popytu mają również ten sam charakter. Również ważną cechą tych charakterystyk jest to, że trend ich przebiegów jest podobny do funkcji stałej energii systemu (E=Fq=constant, rys. 4)., co koreluje z zasadą konserwacji energii. Rysunek 2. przedstawia systemy, których a, b i g są dodatnie (a,b,g >0) lub q=f(F), których a,b,g<0. Dla tych systemów zachowanie tożsamości i/lub istnienia jest bardzo ważne, i dlatego dążą do utrzymania jak najmniejszych zmian. To jest możliwe między innymi poprzez wzrost odpowiednich oporów przeciwko zmianom. Dlatego zachowanie takich systemów jest związane ze wzrostem wewnętrznych i zewnętrznych ciśnień. Odpowiedni wzrost ciśnienia powoduje rozwój gwałtownych zmian, które mogą również prowadzić do zniszczenia systemu i jego otoczenia. Ograniczenie tego wpływu na otoczenie można dokonać poprzez tworzenie różnych rodzajów izolacji. W porównaniu do negatywnych charakterystyk trend przebiegu tych funkcji nie jest zgodny z trendem wyznaczającym przez zasadę konserwacji energii. Systemy takie w największym stopniu przyczyniają się do zmian energii w ich otoczeniu.
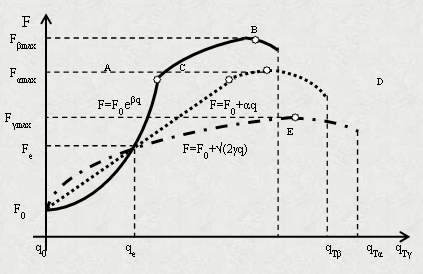
Punkty A, B, C, D i E na rysunku 2. są przykładami centralnych punktów rozmytych przedziałów, gdzie systemy zmieniają swoje elementarne charakterystyki sztywności. W związku z tym pozwalają one w fizyce na rozróżnienie takich charakterystyk, jak: elastycznych i plastycznych. Kiedy odpowiednio duża siła Fmax działa na pewien system charakteryzujący się współczynnikami a,b,g >0, to system ten zmienia te współczynniki na a,b,g<0 (opór systemu na wymuszanie zmian siłą 'F' rozpoczyna maleć), co prowadzi do osłabienia, utraty tożsamości lub zniszczenia systemu. W fizyce koncepcyjne punkty transformacji pozytywnych charakterystyk w negatywne nazywają się "stress breaking" punktami, i są na rys. 2. oznaczone literami B, D i E. W świetle zmian społecznych my nazywamy je chwilami albo zdarzeniami przełomowymi (turning points). Jeżeli efekty zmian w tych punktach są dla nas pozytywne, to często je nazywamy szczęśliwymi chwilami lub przypadkami, natomiast kiedy efekty są negatywne my je uważamy jako terrorystyczne.
Szczególnym przypadkiem jest funkcja proporcjonalnych zmian F=F0+aq, która została użyta przez Newton'a w sformułowaniu drugiego prawa dynamiki. Jeżeli założymy, że F0=F(0)=0, a=m (masa), dq=dv=a=constant (przyspieszenie), to otrzymamy dF/dv=m i F=ma. W tej analizie mechanicznej relacji podmiot-przedmiot, mechaniczna sztywność (dF/dv) ruchu jest stała i równa masie poruszającego się obiektu 'm', która jest interpretowana jako bezwładność tworząca opór przeciwko jej przyspieszeniu i opóźnieniu, natomiast energia jest opisana jako wyrażenie E=óódFdq=óómdvdv=E0+mv2/2 (Sussman GJ et al, 2001). W przypadku, kiedy cząstka o masie 'm' porusza się z prędkością światła w próżni (c=constant), to energia relacji podmiot-przedmiot jest E=ócd(mc)=mc2 dla m należącego do {0,m}. Zaprezentowane podstawowe mechaniczne relacje w formie stałej wartości sztywności (dF/dq=a lub dq/dF=a) są szeroko stosowane we wszystkich dziedzinach naukowych, jak na przykład prawo Hook'a, Ohm'a, liniowa-termiczna rozszerzalność ciał oraz specjalne przypadki funkcji popytu i podaży.
W kontekście społecznych
zjawisk, zachowanie się indywidualnych ludzi, organizacji i społeczeństw, które
charakteryzuje się funkcjami F=F0+aq, F=F0egq,
F=F0+bq2/2 lub F=F0+ (2gq),
gdzie a,b,g >0, jest bardzo popularne. Ponieważ wszystkie społeczne
siły funkcjonują na bazie wzajemnej wymiany różnych czynników materialnych i informatycznych to, to powoduje, że bardzo często one wzajemnie się osłabiają i niszczą oraz tworzą opory przeciwko takiej aktywności. Przykładowo, kiedy
pewna osoba czuje zbliżające się negatywne zmiany, to ona mobilizuje swoje siły
przeciwko nim. Taki proces może reprezentować współzawodnictwo między
osobami, systemami i miedzy systemami i ich otoczeniem. Jednak rozwój współzawodnictwa
poprzez ciągłą eskalację aktywnych i oporowych sił oraz różnego rodzaju ciśnień
prowadzi do terroryzmu i wojen, których kulminacją jest osłabienie i/lub
zniszczenie jednej, kilku lub wszystkich stron tego współzawodnictwa. Ten
proces reprezentuje społeczne przykłady transformacji charakterystyk systemów w zależności od wzrostu zmian i sił społecznych. Szczególnie wyraźnym tego
przykładem we współczesnym świecie jest to, że pod wpływem szybkiego
monotonicznego wzrostu ekonomicznych i politycznych sił, demokratyczne systemy
przekształcają się w autokratyczne powodując rozwój terroryzmu.
(2gq),
gdzie a,b,g >0, jest bardzo popularne. Ponieważ wszystkie społeczne
siły funkcjonują na bazie wzajemnej wymiany różnych czynników materialnych i informatycznych to, to powoduje, że bardzo często one wzajemnie się osłabiają i niszczą oraz tworzą opory przeciwko takiej aktywności. Przykładowo, kiedy
pewna osoba czuje zbliżające się negatywne zmiany, to ona mobilizuje swoje siły
przeciwko nim. Taki proces może reprezentować współzawodnictwo między
osobami, systemami i miedzy systemami i ich otoczeniem. Jednak rozwój współzawodnictwa
poprzez ciągłą eskalację aktywnych i oporowych sił oraz różnego rodzaju ciśnień
prowadzi do terroryzmu i wojen, których kulminacją jest osłabienie i/lub
zniszczenie jednej, kilku lub wszystkich stron tego współzawodnictwa. Ten
proces reprezentuje społeczne przykłady transformacji charakterystyk systemów w zależności od wzrostu zmian i sił społecznych. Szczególnie wyraźnym tego
przykładem we współczesnym świecie jest to, że pod wpływem szybkiego
monotonicznego wzrostu ekonomicznych i politycznych sił, demokratyczne systemy
przekształcają się w autokratyczne powodując rozwój terroryzmu.
Każdy
bardziej złożony system posiada większe możliwości i zdolności do kształtowania
swoich cech sztywności. Jedną z takich zdolności jest możliwość użycia
zaprezentowanych elementarnych typów sztywności zarówno w sposób
indywidualny, jak i złożony. Istnieją dwa podstawowe sposoby rozwoju tych złożonych
charakterystyk: intensywny i ekstensywny. W związku z tym sztywność złożonego
systemu RIs(F)
uformowana w intensywny sposób będzie sumą następujących trzech
elementarnych sztywności IRa(F)= a,
IRb(F)=
a,
IRb(F)= bF i IRg(F)=
bF i IRg(F)= g/F [RIs(F)=
g/F [RIs(F)= a
a bF
bF g/F=(
g/F=( bF2
bF2 aF
aF g)/F i RIs(q)=
g)/F i RIs(q)= bq
bq a
a g/q=(
g/q=( bq2
bq2 aq
aq g)/q].
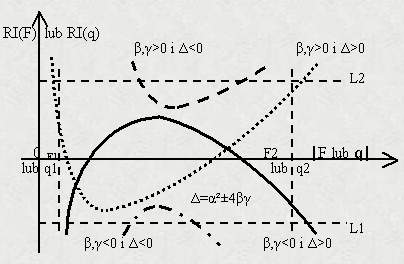
Rysunek 3. pokazuje cztery podstawowe funkcje sztywności złożonego
systemu. Te charakterystyki są odpowiednio określone przez następujące
warunki: (b >0,D<0), (b >0,D >0),
(b<0,D >0) i (b<0,D
g)/q].
Rysunek 3. pokazuje cztery podstawowe funkcje sztywności złożonego
systemu. Te charakterystyki są odpowiednio określone przez następujące
warunki: (b >0,D<0), (b >0,D >0),
(b<0,D >0) i (b<0,D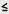 0), gdzie D=a2
0), gdzie D=a2 bg. Na przykład, jeżeli założymy, że przyrosty zmian
'dq' albo sił 'dF' są proporcjonalne do przyrostów czasu 'dt' (dq=adt
lub dF=bdt), to funkcje q(t) i F(t) można interpretować jako funkcje życia
systemów ilustrujące odpowiednio wzrost, istnienie i zniszczenie systemu.
Podstawowe elementy istnienia, to są różnorodne funkcje, które są
realizowane w zależności od wielkości sił i zmian albo w sposób gwałtowny
(rewolucyjny), albo niegwałtowny (ewolucyjny). Szczególnym przypadkiem jest życie
systemu, którego charakterystyka sztywności leży poniżej dolnej granicy, gdyż
jego egzystencja wymaga izolacji i/albo ochrony przed agresywnym otoczeniem
i/lub zwiększenia jego sztywności (opieka, wychowanie i edukacja).
bg. Na przykład, jeżeli założymy, że przyrosty zmian
'dq' albo sił 'dF' są proporcjonalne do przyrostów czasu 'dt' (dq=adt
lub dF=bdt), to funkcje q(t) i F(t) można interpretować jako funkcje życia
systemów ilustrujące odpowiednio wzrost, istnienie i zniszczenie systemu.
Podstawowe elementy istnienia, to są różnorodne funkcje, które są
realizowane w zależności od wielkości sił i zmian albo w sposób gwałtowny
(rewolucyjny), albo niegwałtowny (ewolucyjny). Szczególnym przypadkiem jest życie
systemu, którego charakterystyka sztywności leży poniżej dolnej granicy, gdyż
jego egzystencja wymaga izolacji i/albo ochrony przed agresywnym otoczeniem
i/lub zwiększenia jego sztywności (opieka, wychowanie i edukacja).
Organizmy są szczególnie złożonymi systemami, których różnorodne organy, elementy i procesy funkcjonują w bardziej lub mniej zależny lub niezależny sposób, i dlatego mogą one mieć bardzo różne charakterystyki sztywności w zakresie od sztywnych aż do procesów czy przepływów. Ponadto mają one rozwinięte sposoby zmiany tych charakterystyk. W wyniku tego organizmy mają dużą elastyczność i giętkość (flexibility) w sposobach ich funkcjonowania, na przykład w pewnych warunkach mogą silnie opierać się zmianom, natomiast w innych warunkach mogą łatwo realizować te zmiany. Natomiast w tym procesie u ludzi bardzo ważną rolę spełniają uczucia motywacyjne. Funkcjonowanie złożonych charakterystyk sztywności systemów tworzy bardzo dużą różnorodność w funkcjonowaniu przyrody. Szczególnie istotne zjawisko w tym jest zdolność istnienia substancji w różnych stanach, a dla człowieka istnienie zarówno silnych jak i słabych uczuć motywacyjnych.
3. Ograniczenia systemów i ich charakterystyk
Najbardziej podstawową cechą dowolnej relacji podmiot-przedmiot jest jej ograniczoność,
która wynika z nieustających zmian w przyrodzie. W naszych poprzednich pracach
ideę ograniczeń wyprowadziliśmy z języków, w których istnieją ograniczone
wyrazy i zdania oraz pojęcie 'czas życia', odnoszący się do wszystkich
materialnych systemów. Ogólnie, koncept ograniczeń można uzasadnić w następujący
sposób. Z fizyki wynika, że najbardziej ważnym ograniczeniem jest energia (E=Fq),
wielkość której dla każdego rzeczywistego systemu musi być skończona oraz
różna od zera (Eą0). Kiedy system zwiększa energię, to musi dokonać
inwazję otoczenia, a kiedy system zmniejsza energię, to otoczenie dokonuje
inwazję systemu. Inwazje te zależą od agresywności i wytrzymałości systemu i jego otoczenia. Ponieważ sztywność charakteryzuje również agresywność
relacji podmiot-przedmiot, dlatego możemy powiedzieć: Jeżeli sztywność dF/dq i dq/dF dąży do zera (kiedy F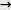 0 i q
0 i q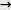
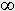 lub q
lub q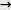 0 i F
0 i F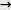
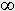 ),
to podmiot opisany przez 'F' staje się niezależny od przedmiotu 'q', i dlatego relacja podmiot-przedmiot {F,q} przestaje istnieć. Ponieważ wszystkie systemy
posiadają cechę oporów, dlatego rzeczywista niezależność zachodzi dla F=Fbl >0
(dolna granica) i q=qtl
),
to podmiot opisany przez 'F' staje się niezależny od przedmiotu 'q', i dlatego relacja podmiot-przedmiot {F,q} przestaje istnieć. Ponieważ wszystkie systemy
posiadają cechę oporów, dlatego rzeczywista niezależność zachodzi dla F=Fbl >0
(dolna granica) i q=qtl
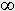 (górna granica) lub dla dolnej granicy qbl >0 i górnej granicy Ftl
(górna granica) lub dla dolnej granicy qbl >0 i górnej granicy Ftl
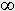 .
Dolną granicę można również nazwać koniecznością, a górną — możliwością.
Kiedy dF/dq i dq/dF są odpowiednio duże efektywność relacji {F,q} staje się odpowiednio tak bardzo mała, że w pierwszym przypadku
prowadzi system do bardzo dużej wewnętrznej i/lub zewnętrznej agresji,
natomiast w drugim przypadku prowadzi do osłabienia systemu a następnie do
jego zniszczenia przez otoczenie.
.
Dolną granicę można również nazwać koniecznością, a górną — możliwością.
Kiedy dF/dq i dq/dF są odpowiednio duże efektywność relacji {F,q} staje się odpowiednio tak bardzo mała, że w pierwszym przypadku
prowadzi system do bardzo dużej wewnętrznej i/lub zewnętrznej agresji,
natomiast w drugim przypadku prowadzi do osłabienia systemu a następnie do
jego zniszczenia przez otoczenie.
Rysunek 4. ilustruje koncepcja podstawowych ograniczeń relacji podmiot-przedmiot albo systemu obserwowanego albo doświadczonego przez człowieka. Przykładowo pole 'ABCD' reprezentuje ograniczenia każdego systemu. Jest ono wyznaczone przez odpowiednie poziomy energii 'E2' i 'E3', wielkość siły Flim i zmian qlim. W rzeczywistości granica tego pola 'ABCD' nie jest ostrą lecz rozmytą oraz bardziej nieregularną linią. W konsekwncji tego w wielu przypadkach występuje trudność w zauważeniu granic, szczególnie dla bardzo elastycznych (flexible) systemów jak na przykład w społecznych systemach i procesach. Ponadto, zależnie od systemu, jego otoczenia oraz rodzaju siły 'F' i zmian 'q', pole 'ABCD' może być różnie ulokowana w przestrzeni{(0-F),(0-q)}.
Załóżmy, że pewien system posiada:
— Pole sił z dwoma biegunami, gdzie jeden charakteryzuje się podmiotowymi, a drugi przedmiotowymi cechami (na
przykład pole ekonomiczne posiadające biegun ludzi bogatych i drugi biegun ludzie biedni),
— 'F' oznacza wypadkową siłę oddziaływania między tymi biegunami powodującą pewne zmiany 'q',
— ograniczenia 'ABCD' jak zaznaczono na rys. 4.
Założenia te redukują analizowany system do prostej relacji podmiot-przedmiot, w której podmiot oddziałuje na przedmiot siłą 'F', wyniku tego zostają zrealizowane zmiany 'q', przy czym wartości 'F' i 'q' nie przekraczają pole 'ABCD'. Jeżeli podmiot działa ze zwiększającą się siłą zgodnie z zaznaczoną drogą 'E=Fq' (rys. 4.), to na tej drodze napotka ograniczenie 'BC', które jest zdeterminowane przez chwilową równowagę między systemem i jego otoczeniem. Przekroczenie tego ograniczenia jest naruszeniem równowagi oraz odzwierciedla inwazję i/albo systemu w stosunku do otoczenia.
Istniejąca silna motywacja wzrostu siły 'F' oraz brak odpowiedniej możliwości i/lub motywacji do inwazji otoczenia powoduje, że system może zwiększać siłę zgodnie z trajektorią 'G1' (rys. 4.). Ten wzrost powoduje wzrost sztywności dF/dq, gdyż podmiot zwiększa agresję w stosunku do przedmiotu, a który zwiększa opór w stosunku do tej siły i do zwiększania zmian 'q'. Sytuacja ta powoduje zwiększenie efektywności działania siły podmiotu. W celu szybkiego zwiększenia tej efektywności najczęściej system dokonuje agresji otoczenia. Jeżeli agresja otoczenia jest niemożliwa, to dalszy wzrost siły 'F' prowadzi w kierunku przekroczenia granicy 'AB' i osiąga punkt przełomowy (turning point). W punkcie tym w analizowanym systemie, siła 'F' traci swoje przedmiotowe cechy, a przedmiot staje się nowym podmiotem. Proces ten tym bardziej jest gwałtowny, im bardziej granica 'AB' będzie przekroczona.
W innym przypadku, kiedy siła 'F' rozwija się zgodnie z trajektorią 'G2' siła ta jest osłabiana, a zmiany zwiększają się. Ten proces osłabia system i pozwala na inwazję systemu przez otoczenie. W celu uniknięcia tego, zmiany 'q' nie mogą osiągnąć ograniczenie 'CD'. Kiedy zmiany osiągną limit 'qlim', system ulega dezintegracji i zniszczeniu.
4. Cykliczne procesy zmian sztywności systemów
Ponieważ zmiany w przyrodzie są nieustające, dlatego systemy, w celu wydłużenia ich czasu egzystencji i/lub tożsamości muszą odpowiednio zmieniać wartości ich parametrów tak, aby nie przekraczały ograniczenia. Takie zmiany są możliwe tylko poprzez odpowiedni przemienne zwiększanie i zmniejszanie wartości parametrów. Taki proces nazywamy cyklicznym procesem zmian, który może być regularny lub nieregularny.
W
odniesieniu do sztywności, cykliczne procesy zawierają zmiany, które
odzwierciedlają zmiany między podmiotowymi i przedmiotowymi cechami elementów
albo zmiany między dodatnimi i ujemnymi charakterystykami systemu. To może być
zapisane jako {+dF/dq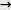 -dF/dq
-dF/dq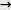 +dF/dq
+dF/dq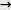 -dF/dq...}
lub {dF/dq
-dF/dq...}
lub {dF/dq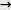 dq/dF
dq/dF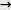 dF/dq
dF/dq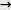 dq/dF...}. Natomiast w odniesieniu do energii, cykliczne procesy mają na celu konserwację
energię (E=Fq=constant) przez system w odpowienio długim okresie czasu.
Idealne procesy cykliczne konserwujące energię są harmonicznymi procesami, w których opór przeciwko przepływowi 'energii' we wszystkich kierunkach
jest równy zeru. Zwykle są one modelowane przy pomocy następującego równania
różniczkowego sztywności Ld2f(t)/dt2+Rdf(t)/dt+f(t)=f0sin(wt+f),
gdzie opór R=0, i wymuszająca funkcja f0sin(wt+f)=0.
dq/dF...}. Natomiast w odniesieniu do energii, cykliczne procesy mają na celu konserwację
energię (E=Fq=constant) przez system w odpowienio długim okresie czasu.
Idealne procesy cykliczne konserwujące energię są harmonicznymi procesami, w których opór przeciwko przepływowi 'energii' we wszystkich kierunkach
jest równy zeru. Zwykle są one modelowane przy pomocy następującego równania
różniczkowego sztywności Ld2f(t)/dt2+Rdf(t)/dt+f(t)=f0sin(wt+f),
gdzie opór R=0, i wymuszająca funkcja f0sin(wt+f)=0.
Szczególnie
liczna klasa ciągłych cyklicznych procesów, która również zawiera rozwiązania
poprzednio wymienionego równania różniczkowego drugiego rzędu, reprezentuje
zbiór funkcji wyznaczonych przez wyrażenie f(t)=f0 f1(t)sin[w(t)t+f]. W tym zbiorze mogą być procesy cykliczne harmoniczne, zbieżne i rozbieżne w zależności od funkcji f1(t), a ich cykle mogą być regularne i nieregularne w zależności od
w(t). Lecz podobnie do monotonicznych procesów, wszystkie wartości
parametrów tych procesów cyklicznych sa odpowiednio ograniczone poprzez górny i dolny limit, jak na przykład amplitudy, częstotliwości i okresy cyklów. W rzeczywistości odpowiednio długi okres
cyklicznego procesu jest dla wielu elementów procesem monotonicznym, natomiast
odpowiednio krótki okres cyklów zmniejsza stabilność elementów odpowiednio
związanych z tym procesem. Jak już wcześniej wspomnieliśmy, zaprezentowana
powyżej metoda modelowania cyklicznych procesów bazująca na czasie tworzy
poważny problem, gdyż usuwa albo ukrywa relacje podmiotowo-przedmiotowe.
Dlatego często między innymi przyczynia się do kształtowania opinii, że w przyrodzie nie istnieje przyczynowość oraz ze względu na silny wpływ języka
na ludzki umysł powoduje to, że w naukach zawsze szuka się relacji albo
korelacji podmiot-przedmiot. Systemy, które najczęściej
funkcjonują w sposób cykliczny, to różnego rodzaju urządzenia
techniczne a w tym silniki.
f1(t)sin[w(t)t+f]. W tym zbiorze mogą być procesy cykliczne harmoniczne, zbieżne i rozbieżne w zależności od funkcji f1(t), a ich cykle mogą być regularne i nieregularne w zależności od
w(t). Lecz podobnie do monotonicznych procesów, wszystkie wartości
parametrów tych procesów cyklicznych sa odpowiednio ograniczone poprzez górny i dolny limit, jak na przykład amplitudy, częstotliwości i okresy cyklów. W rzeczywistości odpowiednio długi okres
cyklicznego procesu jest dla wielu elementów procesem monotonicznym, natomiast
odpowiednio krótki okres cyklów zmniejsza stabilność elementów odpowiednio
związanych z tym procesem. Jak już wcześniej wspomnieliśmy, zaprezentowana
powyżej metoda modelowania cyklicznych procesów bazująca na czasie tworzy
poważny problem, gdyż usuwa albo ukrywa relacje podmiotowo-przedmiotowe.
Dlatego często między innymi przyczynia się do kształtowania opinii, że w przyrodzie nie istnieje przyczynowość oraz ze względu na silny wpływ języka
na ludzki umysł powoduje to, że w naukach zawsze szuka się relacji albo
korelacji podmiot-przedmiot. Systemy, które najczęściej
funkcjonują w sposób cykliczny, to różnego rodzaju urządzenia
techniczne a w tym silniki.
W przyrodzie, wszystkie długo istniejące zjawiska funkcjonują na bazie cyklicznych procesów. W tym również dużo systemów i procesów społecznych funkcjonuje cyklicznie, ponieważ są one częścią względnie długo trwającego zjawiska życia na Ziemi. Właśnie w funkcjonowaniu społeczeństw i społecznych procesów bardzo wyraźnie zauważamy cykliczność różnych. Cykliczność jest związana z uczuciami motywacji, czego szczególnym przykładem jest powtarzalność różnych idei w modzie. Innym interesującym zjawiskiem, którego istnienie wynika z cykliczności jest zjawisko absurdu przesady szczególnie celowo wykorzystywane w dowcipach. Zgodnie z naszymi badaniami, można powiedzieć, że społeczne cykliczne procesy tworzą podstawowe ramy dla wszystkich systemów społecznych, i one w wielkim stopniu determinują trwanie egzystencji i tożsamości społeczeństw, społecznych systemów, organizacji i indywidualnych ludzi. Ponieważ przyroda charakteryzuje się ogromną różnorodnością, dlatego istnieje ogromna liczba różnych cyklicznych procesów, i dlatego istnieje bardzo wiele różnych klas funkcji cyklicznych zarówno empirycznych jak i teoretycznych.
Najważniejszym problemem jaki stoi przed współczesnymi społeczeństwami jest skrajnie silna motywacja, jak i aktywność utrzymania monotonicznego wzrostu populacji ludzi na świecie i ekonomii. Ponieważ jest to sprzeczne z naturalną zasadą cykliczności realizowaną w sposób ewolucyjny przez długotrwałe procesy, dlatego zachodzą i będą się nasilać gwałtowne spontaniczne i zorganizowane procesy mające na celu utrzymania cykliczności w naturalnym otoczeniu, ekonomii i innych społecznych systemach oraz procesach. Dlatego istnieje silne zagrożenie, że taki dalszy rozwój może przekroczyć niebezpieczne ograniczenie inicjując turbulentny społeczny konflikt wśród ludzi oraz między ludźmi a przyrodą.
Pozytywnym społecznym przykładem funkcjonowania stopniowych cyklicznych procesów jest polityczna demokracja, która powoduje regularne cykliczne zmiany rządów. Najważniejszymi cechami demokracji są cykliczne zmiany politycznych dysproporcji w społeczeństwie oraz ograniczenia tych dysproporcji w szczególnym przypadku poprzez elekcję. Jeżeli elekcja funkcjonuje efektywnie, to ogranicza ona siłę rządu i polityków (górne ograniczenie), a zwiększa siłę zwykłych ludzi (dolne ograniczenie). Ponadto, polityczna siła polityków i zwykłych ludzi zmienia się w czasie wyborów, po oraz przed wyborami. W myśl tej prostej koncepcji, możemy powiedzieć, że demokracja albo demokratyczny proces jest procesem, w którym dysproporcje między silnymi i słabymi elementami społecznymi zmieniają się w sposób cykliczny i ewolucyjny. Takie zmiany są możliwe, jeżeli dysproporcje te nie przekroczą pewnego górny i dolny limitu. W związku z tym, ekonomiczną demokrację determinują cykliczne zmiany dysproporcji ekonomicznych między warstwami bogatymi i biednymi, przy czym dysproporcje te nie mogą być przesadnie duże lub małe (Turkiewicz DB and Turkiewicz K, 2003).
Współcześnie, w wyniku globalizacji, ekonomiczne procesy tworzą najsilniejsze pole siły społecznej, i dlatego posiadają największy wpływ na pozostałe pola i procesy. Ponieważ główną ideą współczesnej ekonomii jest stały monotoniczny wzrost jej sił i wyeliminowanie cykliczności, dlatego obecna ekonomia i tak zwany Zachodni świat są niedemokratyczne. Podobnie proces wzrostu populacji ludzi na świecie jest również niedemokratyczny. Dlatego efektywność i istnienie politycznej demokracji oraz ewolucyjne zmiany w społeczeństwach i naturalnym otoczeniu są w poważnym zagrożeniu od wymienionych dwóch bardzo silnych procesów.
5. Zakończenie
Zaprezentowana analiza lingwistycznej relacji podmiot-przedmiot bazująca na sformalizowanych modelach wykorzystujących ciągłe funkcje pokazuje, że ma ona bardzo silny wpływ na wszystkie nauki. Wpływ ten wynika z podstawowego aspektu języka, bez którego nie jest możliwa identyfikacja i zrozumienie dowolnego zjawiska i bez którego nauki nie mogłyby rozwinąć się od obecnej postaci. Ponieważ relacja podmiot-przedmiot jest organicznie i na stałe włączona do ludzkiego umysłu, jest ona używana w sposób automatyczny i podświadomy. Dlatego, pomimo braku świadomości tej relacji, jest ona zawsze podstawowym elementem każdej teorii naukowej oraz ona najbardziej łączy zróżnicowane dziedziny nauki. Oprócz energii również bardzo ważną cechą relacji podmiot-przedmiot sztywność, która pozwala analizować podstawowe zachowanie się wszystkich typów systemów. Jest ona już odpowiednio rozwinięta przez nauki dla pewnych systemów, może ona być rozwinięta lub odnowiona dla innych.
Podsumowując analizę społecznych procesów bazującą na fizykalnym modelowaniu relacji podmiot-przedmiot, możemy powiedzieć, że cykliczne procesy tworzą najważniejszą ramę albo podstawę dla względnie długo-trwałych społecznych procesów i systemów. Monotoniczne procesy przeważnie są ich elementami, są sterowane w adaptacyjny sposób, i dlatego pomijają analizy przyszłości systemów i ich otoczeń. Dlatego taki typ sterowania ułatwia przesadny monotoniczny wzrost systemów, co prowadzi do gwałtownych konfliktów z długo-trwałymi cyklicznymi procesami. Z drugiej strony, antycypacyjny sposób sterowania, który analizuje ewolucyjną cykliczną przyszłość systemów pozwala na silne ograniczenie gwałtownych konfliktów, i dlatego przyczynia się do demokracji wszystkich społecznych procesów.
Literatura
Liboff R.L. (2003). Introductory Quantum Mechanics. 4th Edition, Addison Wesley, New
York.
Sussman G.J., Wisdom J. and Mayer M.E. (2001). Structure and Interpretation of Classical Mechanics. The MIT Press, Cambridge.
Turkiewicz K.,Turkiewicz D.B. (2002). "The Role of the Structure of the Conditional
Sentence in Sciences", The XVth ISA World Congress of Sociology Brisbane,
Australia, July 7-13.
Turkiewicz D.B., Turkiewicz K. (2003). „Holistic Analysis of the Physical
Nature of Democracy and Terrorism", in InterSymp 2003, The 15th International Conference on
System Research, Informatics and Cybernetics, Baden-Baden, Germany, July
28-August 2.
Wittgenstein L. J. (1961). Tractatus Logico Philosophicus. Routledge and Kegan Paul, London.
Ninijesza praca pod tytułem 'Formalised Synthetic Modelling of Subject — Object Relations' została opublikowana w „CASYS, International Journal of Computing Anticipatory Systems" wydawanym przez D.M.Dubois, w maju 2004.
| Kazimierz i Domenika B. Turkiewicz Naukowcy z Australii; Mater Misericordiae Hospital, The University of Queensland, Brisbane. Number of texts in service: 3 Show other texts of this author |
Original.. (http://therationalist.eu.org/kk.php/s,3779)
(Last change: 30-11-2004)