
|
Philosophy » » Ancient philosophy Bractwo pitagorejskie [3] Koncepcja transmigracji dusz, może mieć jednak pewną wartość dla zmiany naszego sposobu traktowania zwierząt. Ksenofanes opisywał jak Pitagoras widząc człowieka bijącego psa, nakazał mu zaprzestanie, gdyż rozpoznał w skowycie psa głos swego przyjaciela. Pies jest na ogół wierniejszym przyjacielem człowieka niż inny człowiek, Pitagoras z pewnością się nie mylił. Oczywiście nie tylko psy zasługują na lepsze traktowanie. Zresztą, nie tylko zwierzęta, ale wszystko co żyje — cała nasza przyroda jest w wielkim niebezpieczeństwie. Atakuje ją wielki wróg: człowiek... Nauka o duchu a duch naukiPitagoras wtajemniczony był nie tylko w orfizm, ale i w misteria apollińskie. Jego doktryna religijna była syntezą ich obu. Pierwiastek apolliński, w przeciwieństwie do pierwiastka dionizyjskiego łączonego z uczuciami, utożsamiany jest z rozumem. Znalazło to doskonałe odzwierciedlenie u pitagorejczyków. Jeśli istnieje jakiś idealny model relacji wiary religijnej i nauki, to jest to model pitagorejski: Każdy człowiek został stworzony przez Boga w tym celu, ażeby poznawać i oglądać. Fenomen ich wierzeń religijnych polegał na tym, iż w odróżnieniu od innych grup mistycznych, które praktykowały jako środki mistyczne muzykę, tańce oszałamiające czy wino, pitagorejczycy za najważniejsze środki oczyszczania duszy uznawali życie ascetyczne, muzykę i pracę naukową. Dla wielu z nich ten ostatni stawał się najważniejszym, w efekcie czego w V w. doszło do rozłamu. Grupa, którą określa się mianem „akuzmatyków", koncentrowała się na wątkach mistycznych i sakramentalnych. Natomiast tzw. matematycy (od mathéma 'nauka, umiejętność'), pozostając przy dawnych wierzeniach, na głównym planie stawiali naukę. Jednak nauka jako środek oczyszczenia nie stanowił dla nich sposobu do osobistego wyróżnienia się. Dla współczesnych naukowców jest to bardzo ważny i stymulujący aspekt badań, zupełnie zrozumiały i pozytywny, choćby w tym sensie, że przez skromność pitagorejskich uczonych dziś nie znamy wiele ich nazwisk ani tego kto czego dokonał. Jako przyczynę tego, wielu skłonnych byłoby wskazać tajemnicę jaką mieli pitagorejczycy otaczać swe nauki. Krążyło np. podanie o tym jak jeden z adeptów sekty został przez braci utopiony za to, że wyjawił obcym odkrycia dotyczące liczb. Są to jednak zapewne legendy. Związek pitagorejski prawdopodobnie składał się z dwóch kategorii członków: właściwych „pitagorejczyków" (pythagoreioi), którzy tworzyli wspólnotę sensu stricto (wspólnota dóbr, wspólne zamieszkiwanie, noszenie białych szat, przestrzeganie tabu), oraz „pytagorystów" (pythagoristai), którzy zbierali się jedynie dla wysłuchiwania wykładów Pitagorasa. Na podstawie Jamblicha, ten podział możemy utożsamić z podziałem na matematyków i akuzmatyków. J. Brosse przedstawia ten podział jako „krąg zewnętrzny", czyli akuzmatycy, którzy mieli za zadanie obronę związku, tworzyli konfraternię wojowników dowodzonych przez Milona z Krotony, zięcia Pitagorasa, oraz „krąg wewnętrzny", czyli matematycy, wtajemniczeni m.in. w prazasadę liczb. [ 9 ] Pytagoryści-akuzmatycy nie tylko nie zajmowali się pracą naukową, ale z czasem do słów Mistrza zaczęli pochodzić z nabożną czcią, traktując je jako dogmaty (podobnie jak w Średniowieczu traktowano Arystotelesa). Wśród nich za mędrca nie uchodził ten, kto dokonał osobiście najwięcej, lecz ten kto spamiętał więcej z nauk Guru. To oni przyczynili się do ubóstwienia Pitagorasa oraz rozrostu legend pitagorejskich. Jest to postawa zupełnie przeciwna duchowi naukowemu i podobnie jak neopitagoreizm, akuzmatycy stanowią ten nurt w łonie Pitagoreizmu, który nie zasługuje na nasze większe zainteresowanie. Na temat relacji wiara-nauka w Pitagoreizmie, niezwykle istotna i celna jest uwaga Bertranda Russella: "Niezależnie od elementu mistycznego, wywodzącego się z odżywającego ruchu orfickiego, naukowy aspekt działalności szkoły nie został przyćmiony przez jej koncepcje religijne. Nauka nie nabrała posmaku religii, choć pragnienie poświęcenia się teoriom uznano za coś religijnego." [ 10 ] Wielu późniejszych naukowców wyrażało się o swoim stosunku do nauki w podobnym duchu. Oczywiście absurdalne i złośliwe jest przedstawianie tego jako „religii nauki", czym do znudzenia bałamucą swoich czytelników religijni apologeci i inni przeciwnicy nauki. Posłuchajcie fragmentu popularnonaukowego wykładu Feynmana: „Tej pracy [tj. badań i odkryć] nie wykonuje się dla korzyści płynących z wdrażania w życie nowych osiągnięć. Motywem są emocje związane z odkryciami. Być może, większość was o tym wie. Jest jednak niemal niemożliwe przekazanie podczas wykładu tym z was, którzy tego uczucia nie znają, owego ważnego aspektu pracy naukowej, jej ekscytującej strony, prawdziwego powodu, dla którego ludzie zajmują się nauką. A nie rozumiejąc tego, gubicie istotę rzeczy. Nie możecie pojąć nauki ani jej związku z czymkolwiek innym, dopóki nie zrozumiecie i nie docenicie tej wielkiej przygody naszych czasów. Nie żyjecie pełnią swojej epoki, jeśli nie rozumiecie z jak wielką przygodą — a przy tym szalonym i podniecającym przedsięwzięciem — macie do czynienia. Myślicie, że nauka jest nudna? Nie, nie jest." Innym razem mówił: „Kiedy taki obiektywny obraz zostaje w końcu skonstruowany, a tajemnica i majestat materii widnieją przed nami w całej krasie, wtedy przyjrzenie się z powrotem człowiekowi jako skupisku materii, potraktowanie życia jako części uniwersalnej, najgłębszej tajemnicy przynosi doznanie, które jest bardzo rzadkie i niezwykle poruszające. Zwykle kończy się to śmiechem i refleksją nad daremnością usiłowań zmierzających do zrozumienia, czymże jest ten atom we Wszechświecie. Czymże jest ta istota — atom obdarzony ciekawością — który przygląda się sobie i zastanawia, dlaczego w ogóle się zastanawia? Zwykle takie naukowe rozważania prowadzą do przerażenia i tajemnicy, do zagubienia na granicy niepewności. Wydają się jednak tak głębokie i tak istotne, że teoria zakładająca, że wszystko to jest sceną, na której Bóg obserwuje ludzkie zmagania z dobrem i złem, okazuje się niewystarczająca. niektórzy powiedzą, że przed chwilą opisałem doświadczenie religijne. Bardzo dobrze. Możecie to nazywać jak chcecie. Powiem wtedy, że dzięki przeżyciu religijnemu tego rodzaju młody człowiek przekonuje się, iż religia wyznawana w jego Kościele nie wystarczy, by opisać, by ogarnąć podobne doświadczenie. Bóg tego Kościoła nie jest dość potężny." [ 11 ] Wilson w swej Konsiliencji nazywa to „jońskim zauroczeniem". Moim zdaniem słuszniejszym i bardziej adekwatnym określeniem byłoby "pitagorejskie zauroczenie". Jak powiada Jacob Bronowski: „Kiedy Pitagoras dowiódł swego wielkiego twierdzenia, złożył muzom w ofierze sto wołów w podziękowaniu za natchnienie. Był to gest dumy i pokory zarazem, uczuć jakie po dziś dzień odczuwa każdy uczony, gdy otrzymane dane liczbowe pasują do siebie i powiadają: Oto fragment struktury samej przyrody, klucz do niej." Pitagorejski ośrodek badawczyGłówny rozkwit naukowy w łonie Pitagoreizmu wiąże się z czasem tzw. młodych pitagorejczyków (przełom V i IV w. p.n.e.), już po upadku pierwszej szkoły w Krotonie. Do najwybitniejszych młodopitagorejczyków zaliczamy Archytasa z Tarentu i Timajosa z Lokri. W kolejnych generacjach wyróżnił się Eudoksos z Knidos. Filolaos i Eurytas eksportowali Pitagoreizm do Grecji, zakładając związek w Tebach. Ich uczeń, Ksenofil, założył szkołę pitagorejską w Atenach. Głównymi dziedzinami, jakimi zajmowały się szkoły pitagorejskie były:
Jest to wszelako nasz podział. Pitagorejczyk powiedziałby, że oprócz medycyny ich nauka zajmuje się matematyką, a tutaj: a) geometrią, b) geometrią stosowaną (za jaką uważali astronomię), c) arytmetyką, d) arytmetyką stosowaną (za jaką uważali muzykę). Największy powód do chluby dała im szkoła matematyczna, (która z pewnością zawdzięczała wiele Babilończykom), dorównując swej sławie szkole medycznej z wyspy Kos (w koskiej szkole działał m.in. Hipokrates). Arystoteles pisał: „Tak zwani pitagorejczycy zajęli się pierwsi matematyką i pchnęli ją naprzód". Nie znaczy to, że wcześniej ludzie nie umieli liczyć i rachować. Pitagorejczycy stworzyli matematykę jako dziedzinę naukową, podczas gdy wcześniej funkcjonowała w sferze praktyki. Tym samym jeśli ktoś miałby być patronem matematyków, to Pitagoras jest najlepszym kandydatem. Badanie figur i stosunków przestrzennych (geometria)
Oni też odkryli regułę "złotego podziału" mówiącą, jak należy ustalić proporcje elementów dzieła plastycznego, by dawały najlepszy skutek estetyczny. Nauka o liczbach (arytmetyka)Należy przede wszystkim zaznaczyć, że pitagorejskie pojęcie liczby nie było tak abstrakcyjne jak nasze, traktowali je łącznie z wielkościami przestrzennymi, liczba była rozumiana zawsze jako przestrzenna wielkość (od tego do dziś pozostała nazwa liczb „kwadratowych"). Zajmowali się klasyfikacją liczb. Wprowadzili takie rozróżnienia, jak liczby parzyste i nie, będące kwadratami i nie. Liczby kwadratowe to sumy kolejnych liczb nieparzystych (np. liczba kwadratowa 9 jest sumą: 1+3+5, nazwa wzięła się z przedstawiania tych liczb pod postacią kwadratów stworzonych z kamyków). Natomiast sumy kolejnych liczb parzystych nazywali liczbami prostokątnymi. Specjalne znaczenie miała suma pierwszych czterech liczba naturalnych (1+2+3+4) — tzw. tetraktys (arcyczwórka lub czwórnia). Układana z kamyków w kolejnych rzędach przybierała postać trójkąta (liczba trójkątna) i była ich liczbą świętą. Odróżniali także liczby niewymierne (niedające się zapisać w postaci ułamka). Liczby niewymierne odkryli dzięki stosowaniu liczb w odniesieniu do geometrii: stwierdzili, że stosunek długości przekątnej kwadratu do długości jego boku nie jest równy stosunkowi 2 liczb całkowitych.
Footnotes: [ 9 ] J. Brosse, Mistrzowie
duchowi, Katowice 2000, s.169. [ 10 ] B. Russell, Mądrość
Zachodu, Warszawa 1995, s.21. [ 11 ] R.P. Feynman, Sens
tego wszystkiego, Warszawa 1999, s.15-16, 37. « Ancient philosophy (Published: 30-11-2003 Last change: 07-02-2005)
page 3106 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [ Cooperation ] [ Advertise ] [ Map of the site ] [ F.A.Q. ] [ Store ] [ Sign up ] [ Contact ] The Rationalist © Copyright 2000-2018 (English section of Polish Racjonalista.pl) | ||


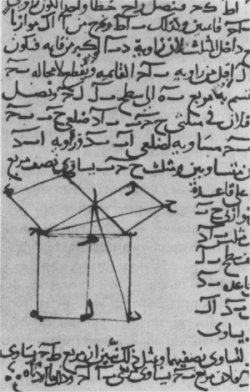 Odkryli dwa najważniejsze elementarne twierdzenia: o
sumie kątów w trójkącie (jednak twierdzenia te dowodzili oddzielnie dla
trójkątów równobocznych, równoramiennych i nierównoramiennych) oraz tzw.
twierdzenie Pitagorasa: pole kwadratu zbudowanego na przeciwprostokątnej trójkąta
prostokątnego jest równe sumie pól kwadratów zbudowanych na przyprostokątnych:
c2 = a2 + b2. Od nich pochodzą takie pojęcia
jak „parabola", „hiperbola", „elipsa".
Odkryli dwa najważniejsze elementarne twierdzenia: o
sumie kątów w trójkącie (jednak twierdzenia te dowodzili oddzielnie dla
trójkątów równobocznych, równoramiennych i nierównoramiennych) oraz tzw.
twierdzenie Pitagorasa: pole kwadratu zbudowanego na przeciwprostokątnej trójkąta
prostokątnego jest równe sumie pól kwadratów zbudowanych na przyprostokątnych:
c2 = a2 + b2. Od nich pochodzą takie pojęcia
jak „parabola", „hiperbola", „elipsa".
 Redaktor naczelny Racjonalisty, założyciel PSR, prezes Fundacji Wolnej Myśli. Autor książek
Redaktor naczelny Racjonalisty, założyciel PSR, prezes Fundacji Wolnej Myśli. Autor książek