
|
Science » Astronomy » Maska Coudera i figuryzacja zwierciadła [1] Maska Coudera pozwala na podzielenie zwierciadła na strefy, które można pomierzyć ilościowo. Nie należy dzielić zwierciadła na zbyt wiele stref - lepiej posiadać wiarygodne odczyty z mniejszej liczby stref, niż zbyt wiele, mniej wiarygodnych danych. Poniżej zamieściłem maskę Coudera dla zwierciadła o średnicy 203 mm. 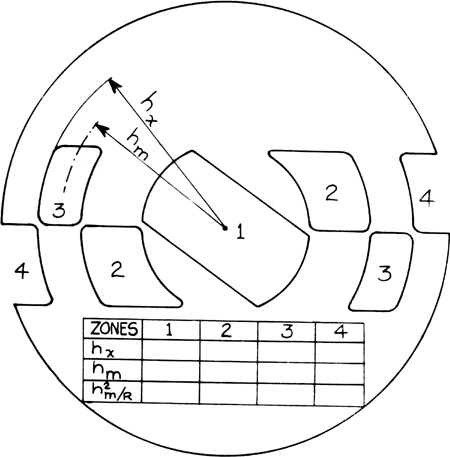 Rycina 50. Maska Coudera. Kliknij tutaj, aby uzyskać maskę dostosowaną do zwierciadła o średnicy 203 mm. Po wydrukowaniu wytnij dokładnie wszystkie strefy i zmierz je bardzo dokładnie. Hx to odległość od środka do zewnętrznej krawędzi strefy (promień zewnętrzny), Hm to odległość od środka do środka strefy (promień wewnętrzny). Drugim sposobem uzyskania Hm jest zmierzenie Hx i krawędzi wewnętrznej strefy, dodanie ich i podzielenie przez 2. Dla ułatwienia orientacji podczas testów można obciąć około 1/4 górnej części maski. Wartość w najniższym wierszu można zignorować, gdyż będzie obliczana automatycznie przez oprogramowanie (na podstawie Texereau [ 1 ]) Pomiary należy wykonać po co najmniej godzinie — dwóch od momentu postawienia zwierciadła na stojaku. Jest bardzo ważne, aby jego temperatura zrównała się z otoczeniem. Najpierw upewnij się, że krawędź noża wędruje wzdłuż osi optycznej zwierciadła i sprawdź sekwencję obrazów. Następnie zakryj zwierciadło maską Coudera i poczekaj około 15 minut, aż uspokoi się powietrze. Jedną ręką trzymamy pokrętło wzdłużne, drugą ręką pokrętło poprzeczne i wprowadzając i wyprowadzając ostrze w oś optyczną oceniamy stan wygaszenia każdej strefy z osobna. Noża nie trzeba zerować, gdyż tak naprawdę nie liczy się sama wartość odczytana ze skali, lecz różnica w wartości pomiędzy poszczególnymi strefami. Numery powinny rosnąć od strefy Z1 do Z4. Najtrudniej jest odczytać środkową strefę i zajmuje wiele czasu i praktyki aby wyczulić oko na te zmiany. Czego właściwie szukamy? Celem jest znalezienie punktu na podziałce dla każdej strefy na osi podłużnej, w którym wygasa ona natychmiast po wprowadzeniu noża. Cała strefa musi zaciemnić się jednorodnie, bez wędrujących cieni z jednego końca na drugi. W przypadku stref Z2, Z3, Z4 obie strony maski Coudera powinny wygasnąć jednocześnie. Zanim zaczniesz spisywać numery z podziałki, staraj się poćwiczyć „na sucho", wygaszając kolejno strefy Z1 — Z4 i z powrotem. Tak jak wspominałem — najtrudniejsza do oceny jest strefa Z1 i najlepiej jest przesunąć wpierw nóż w kierunku zwierciadła, obserwując wędrujący cień i stopniowo cofać ostrze aż do momentu, gdy cała strefa wygasza się w jednym momencie. Najbardziej wiarygodny odczyt jest zawsze ze strefy Z3, czyli obszaru 0,7 średnicy zwierciadła i te dane, nie zaś wartość strefy Z1, traktowane są przez oprogramowanie jako punkt odniesienia. 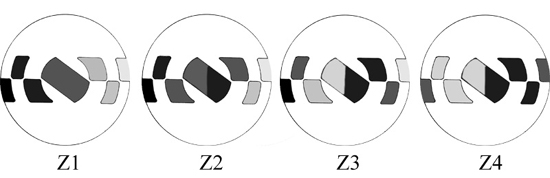 Rycina 51. Odczyty z maski Coudera poszczególnych stref. W przypadku stref Z2, Z3 i Z4, każda z nich musi wygasnąć jednocześnie po obu stronach. Oczywiście, wszystkie obliczenia można wykonywać ręcznie, jednak szczerze odradzam — są one zbyt czasochłonne. Ciekawych odsyłam do książki Texereau [ 1 ]. My tymczasem użyjemy doskonałego oprogramowania freeware, które pozwoli nam ułatwić wyzywający proces figuryzacji. Program nazywa się FigureXP i można go sciągnąć tutaj: FigureXP. Poniżej znajduje się ekran (Setup, F2), w którym wprowadza się dane. 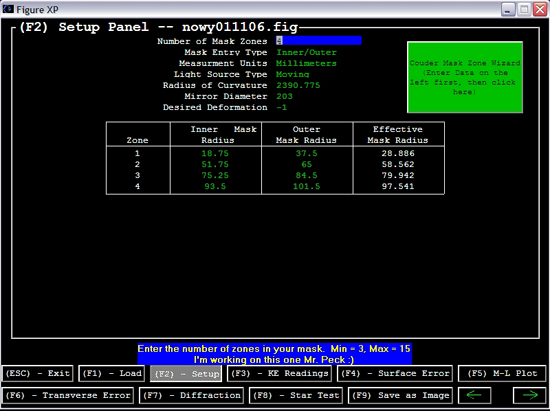 Rycina 52. FigureXP to bardzo użyteczny i prosty w obsłudze program. Po uruchomieniu wybieramy 'Create new file', aby stworzyć nowy plik lub ładujemy z dysku poprzednio używany. Po wciśnięciu F2 pojawia się panel Setup w którym kolejno wpisujemy potrzebne dane. Porównaj z poniższym tekstem. Ekran 'Setup' posiada następujące opcje:
Gdy wpiszemy wszystkie dane przechodzimy do następnego panelu za pomocą F3. 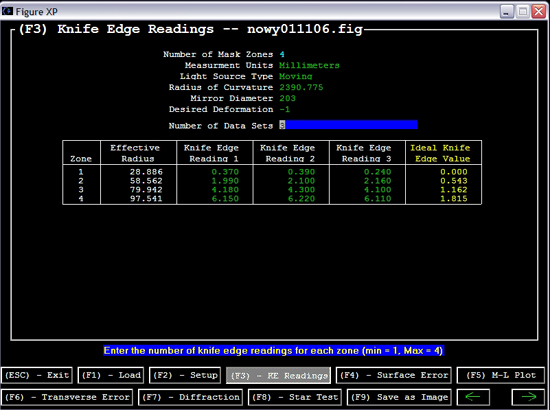 Rycina 53. Panel 'KE Readings', czyli odczyty z krawędzi noża. Wyjaśnienie poniżej. Pojawia się następna opcja — ilość odczytów (number of data sets). Ponieważ ludzkie oko nie jest doskonałe i w naszych danych zawsze będzie pewien błąd, należy wykonać co najmniej trzy odczyty każdej strefy, które zostaną uśrednione. Z biegiem czasu można dojść do takiej wprawy, że odczyty z Z3 strefy będą identyczne do 2 miejsca po przecinku! Ja zawsze wykonywałem trzy odczyty — zaczynając od strefy Z1 do Z4, z powrotem od Z4 do Z1 i ponownie od Z1 do Z4. Staraj się nie patrzeć na poprzednie odczyty, aby się nimi nie sugerować. Gdy już będziesz naprawdę blisko ukończenia zwierciadła, po odczytaniu danych, przekręć zwierciadło o 90 stopni, przykryj ponownie maską Coudera, odczekaj 15 minut i powtórz odczyty. Uzyskane dane wpisujemy dla każdej strefy do tabeli. Po prawej stronie, żółtym kolorem, podane są wartości idealne dla każdej z nich. Gdy wpiszemy nasze odczyty, przechodzimy do kolejnego panelu, wciskając, F4. 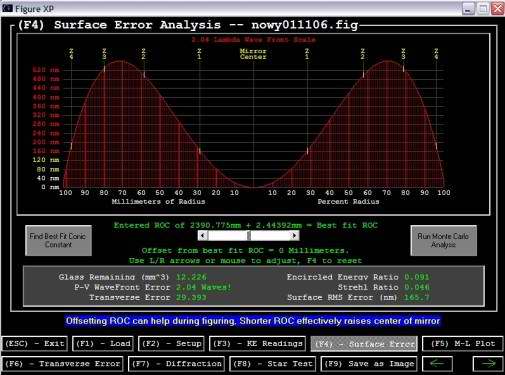 Rycina 54. Panel 'Surface Error', czyli błąd powierzchni. Poszczególne strefy oznaczone są Z1, Z2, Z3 i Z4. Pamiętaj, że wykres nie reprezentuje kształtu zwierciadła, lecz odchyłkę każdej ze stref od wartości idealnej. Celem jest więc „spłaszczenie" wykresu, czyli wyrównanie stref jak najbliżej do ich wartości idealnych. Powyższy wykres i dane z Ryc. 53 pochodzą z mojego pierwszego odczytu, który jak widać, reprezentuje monstrualną hiperbolę. Powyższy panel reprezentuje błąd powierzchni zwierciadła, oś pozioma to odległość od środka, oś pionowa reprezentuje odchyłkę krzywizny w nanometrach (nm). Na samej górze wyrażona jest skala w długościach fali świetlnej. Dla nas na tym panelu najważniejsze są dwie rzeczy: kształt krzywej i wartość błędu wyrażona w długości fali (lambda) — 'P-V Wavefront Error'. Spójrzcie na powyższy wykres — olbrzymi wulkan, z dziurą w środku i stromymi krawędziami! Odchyłka od prawidłowej figury wynosi ponad dwie długości fali! ('P-V Wavefront Error' 2.04 Waves!) Kiedy klikniemy na przycisk po lewej 'Find best fit conic constant', pokazuje się wartość -3.2, czyli wielgachna hiperbola. Co właściwie oznacza 'odchyłka równa x fali'? 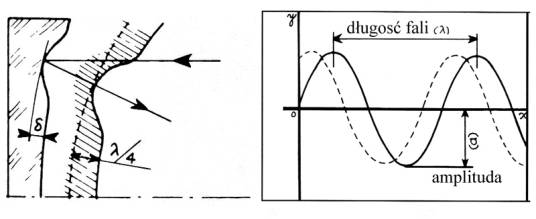 Rycina 55. Zwierciadło teleskopowe nie może mieć odchyłki od prawidłowej figury większej niż 1/4 lambda. Po prawej przedstawiona jest schematycznie fala świetlna oraz przesunięcie 1/4 długości. Gdy błąd jest większy, fala odbita może osłabić falę nadchodzącą w procesie zwanym interferencją (fale pokrywające się grzbietami, wzmacniają się, przesunięcie fali spowoduje osłabienie jednej fali przez drugą, gdyż ich grzbiety staną naprzeciw siebie). Zwierciadło zatem musi spełnić tzw. kryterium Rayleigha, którzy obliczył, że 1/4 fali światła, na które ludzkie oko jest najbardziej wrażliwe wynosi 140 nm (nanometrów). Załóżmy, że błąd powierzchni posiada głębokość delta (schemat po lewej), jest to dodatkowy dystans, który światło musi pokonać w kierunku do i od zwierciadła. Dlatego też całkowite opóźnienie wywołane przez defekt ma wartość 2*delta, czyli błąd powierzchni zostaje tak naprawdę podwojony. Dlatego też, aby zwierciadło spełniało kryterium Rayleigha, defekt powierzchni nie może przekroczyć 140/2 = 70 nanometrów (0,000 070 mm). Dowód na to, że manipulacja na tak niewyobrażalnie małych wartościach jest możliwa znajdziecie poniżej. (na podstawie Texereau [ 1 ]) Zwierciadła komercyjne powinny mieć odchyłkę maksimum 1/4 fali, my jednak chcemy wykonać zwierciadło doskonałe i nie powinniśmy kończyć figuryzacji zanim nie uzyskamy błędu mniejszego niż 1/10 fali. Jeśli zdecydowałeś się na wykonanie zwierciadła do obserwacji głównie planet, twoim celem powinno być nawet 1/16 fali. Proces poprawek jest za każdym razem inny i zależy od twardości polerownika, temperatury stanowiska pracy, doświadczenia operatora etc. Podstawą jest ostrożność, odpowiednia analiza i zrozumienie własnych poczynań. Figuryzacji trzeba poświęcić dużo czasu. Należy prowadzić skrupulatne notatki z każdego odczytu i pracować powoli i sukcesywnie. Dobrze jest włączyć sobie po kolei profile zwierciadła na ekranie i analizować w jaki sposób nasze działania wpłynęły na zmianę kształtu. Cały proces jest jak próbowanie złapania czterech kotów jedną ręką na raz. Kiedy mamy już trzy w garści i sięgamy po czwartego, drugi wypada z ręki i ucieka. Podczas podnoszenia drugiego, wypadają dwa kolejne etc. Samemu zdarzyło mi się raz, że trzy strefy miały wartość idealną, pozostała czwarta była zaś zupełnie poza kontrolą. Poniżej przedstawiam kilka przykładowych rycin, które reprezentują kolejne kroki moich zmagań podczas figuryzacji. W każdym przypadku skutek danego ruchu może być inny ze względu na różnice pomiędzy polerownikiem. Ważnym jest więc uchwycenie jego działania w toku figuryzacji.
Footnotes: [ 1 ] Jean Texereau, How to Make a Telescope,
Second Edition, wydawnictwo Willmann-Bell, Inc., ISBN 0-943396-04-2. Wydawca
zezwala na reprodukcję, tłumaczenie i modyfikację ilustracji tylko na
zasadzie fair use, czyli w celach edukacyjnych i niedochodowych. Szczegóły
tego prawa można przeczytać w sekcjach 107 i 108 dokumentu United States
Copyright Act. « (Published: 12-06-2006 Last change: 17-06-2006)
page 4846 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [ Cooperation ] [ Advertise ] [ Map of the site ] [ F.A.Q. ] [ Store ] [ Sign up ] [ Contact ] The Rationalist © Copyright 2000-2018 (English section of Polish Racjonalista.pl) | ||



 Ukończył biologię molekularną na Uniwersytecie Adama Mickiewicza w Poznaniu. Pracował jako Research Specialist in Health Science w Department of Anatomy and Cell Biology na University of Illinois w Chicago. Obecnie pracuje jako Associate Cell Biologist / Histologist w Abbott Laboratories (Illinois). Specjalizuje się w ekspresji białek 'od zera', hodowlach linii komórkowych, symulacji in vitro procesów zachodzących w komórkach. Jego pasją jest teoria ewolucji, w szczególności ewolucja systemów biochemicznych i pochodzenie życia we Wszechświecie.
Ukończył biologię molekularną na Uniwersytecie Adama Mickiewicza w Poznaniu. Pracował jako Research Specialist in Health Science w Department of Anatomy and Cell Biology na University of Illinois w Chicago. Obecnie pracuje jako Associate Cell Biologist / Histologist w Abbott Laboratories (Illinois). Specjalizuje się w ekspresji białek 'od zera', hodowlach linii komórkowych, symulacji in vitro procesów zachodzących w komórkach. Jego pasją jest teoria ewolucji, w szczególności ewolucja systemów biochemicznych i pochodzenie życia we Wszechświecie.