TRZY PUŁAPKI

Licytacja o dolara

Dwaj gracze konkurują o leżącego na stole dolara. Konkurencja ma formę licytacji z postąpieniem 25 centów. Po zakończeniu licytacji obaj płacą ostatnio zalicytowane kwoty, a zwycięzca bierze dolara. Pierwszy licytuje 25 centów, oczekując, że zarobi 100, wyda 25, a więc zyska 75 centów. Drugi ma teraz do wyboru albo nic nie stracić i nic nie zyskać, jeśli spasuje, albo zalicytować 50 centów i zyskać 100 — 50 = 50 centów. Wtedy pierwszy traci zalicytowane 25 centów, jeśli pasuje, lub licytując 75 centów zyskuje 100 — 75 = 25 centów. Teraz drugi albo, pasując, traci ostatnio zalicytowane 50 centów, albo licytuje 100, nic nie zyskując (100 — 100 = 0), ale też nic nie tracąc. Następnie pierwszy musi zdecydować, czy stracić 75 centów, czy tylko 25, gdyby zalicytował 125. Oczywiście, woli zminimalizować stratę, i licytuje 1 dolar 25 centów. Przepłaca działając w dobrze pojętym własnym interesie. Kolejny ruch drugiego jest również paradoksalny, gdyż albo pasuje i traci dolara, którego zalicytował, albo traci tylko pół dolara, jeśli podniesie licytację do półtora: wtedy zapłaci 150 centów, ale odzyska 100, więc jego strata się zmniejszy.

Ta gra nie ma końca. Kiedy pierwszy zalicytuje milion dolarów, drugiemu wciąż się opłaca go przebić. W rzeczywistych eksperymentach gracze na ogół licytują do 3 — 4 dolarów. Przegrywają wszyscy, mimo że suma gry jest dodatnia i wszyscy mogliby się nią podzielić.

Licytacja o dolara może być traktowana jako model przetargu handlowego o kontrakt wart dolara lub wyścigu zbrojeń, w którym dwa konkurujące państwa zbroją się w celu zagarnięcia spornego terytorium o wartości dolara. Działając w każdym ruchu racjonalnie, zwiększają wydatki zbrojeniowe w nieskończoność.

Dylemat więźnia

Śledczy zatrzymuje dwóch włamywaczy, co do których ma tak zwaną operacyjną wiedzę, że obrabowali bank, lecz nie może znaleźć wystarczających dla sądu dowodów. Jeśli któryś z podejrzanych nie zacznie współpracować, śledczy będzie musiał ich wypuścić — mimo przekonania o winie. Zamyka ich zatem w osobnych celach i osobno przesłuchuje, każdemu składając identyczną ofertę:

TN jeśli się przyznasz i oskarżysz kolegę, wtedy jako świadek koronny wyjdziesz na wolność, a dla niego zażądam 10-letniego wyroku;

TT jeśli ty się przyznasz i twój kolega też się przyzna, wtedy świadka koronnego nie potrzebuję, ale zważywszy na waszą współpracę — zażądam tylko po pięć lat dla każdego;

NT jeśli się nie przyznasz, a twój kolega cię oskarży, to on wyjdzie na wolność,
ty zaś dostaniesz 10 lat;

NN jeśli obaj się nie przyznacie, może nic wam nie udowodnię, ale przytrzymam każdego
w areszcie przez rok.

Oczywiście, w interesie obu jest nie przyznać się (wariant NN), lecz w interesie każdego z osobna jest całkowite uniknięcie kary, co może osiągnąć tylko oskarżając drugiego. Pierwszy wybierze zatem TN, oskarżając drugiego, a drugi NT, oskarżając pierwszego. Jednak oba te warianty składają się na wariant TT, w którym oskarżeni są obaj, a zatem obu grożą pięcioletnie wyroki. Wariant solidarny (NN), mimo że optymalny, stwarza równocześnie największe zagrożenie, bo aż 10-letnim wyrokiem w przypadku zdrady wspólnika.

Każdy więzień musi zdecydować, czy odmówić współpracy ze śledczym, co mu grozi rocznym lub 10-letnim wyrokiem, czy pójść na współpracę i zmniejszyć zagrożenie do 0 lub 5 lat. Racjonalnie rzecz biorąc, jeśli ma wątpliwości co do postawy wspólnika, wybierze to drugie: przyzna się.

Gdyby więźniowie mogli się komunikować, nawiązaliby współpracę w celu osiągnięcia optimum gry, czyli dwóch „osobolat" więzienia. Brak kooperacji przesuwa wynik gry na dziesięć „osobolat".

Dylemat więźnia jest bardzo ważnym przykładem gry niekonkurencyjnej, o sumie niezerowej. Wielka liczba istotnych modeli sprowadza się w ten czy inny sposób do tej właśnie gry.

Entuzjaści dylematu więźnia organizują turnieje programów komputerowych, grających wielokrotnie w tę grę. Do tej pory w turniejach tryumfuje prosty program, kierujący się następującą filozofią:

— w pierwszej grze kooperuj, nie zdradzaj, a potem:

— rób to, co on poprzednio: jeśli cię zdradził — zdradź, jeśli kooperował — kooperuj.

Niektórzy traktują to jako przesłanie moralne: bądź przyjazny, kooperatywny, karz zdrajców, ale jeśli się poprawią, nie bądź pamiętliwy.

Ginące pastwisko

Przykład ginącego pastwiska jest odpowiednikiem wieloosobowego dylematu więźnia. Rozważmy wieś składającą się z dziesięciu zagród, użytkujących wspólnie pastwisko, którego nie da się podzielić. W jednej jego części jest woda, w innej cień, w innych trawa, koniczyna i rozmaite rzeczy dobre dla krowy. Przyjmijmy, że nie istnieje sposób rozdzielenia tego pastwiska na pełnowartościowe części. Pastwisko może wyżywić 10 krów, z których każda przynosi rocznie 1000$ zysku. Większa liczba krów zmniejsza zyski, bo krowy są niedożywione, i tak gdy jest ich 11, to każda daje po 900$ zysku, gdy 12 — to po 800$, i tak dalej aż do 19, z których każda przynosi po 100$, a przy wprowadzeniu dwudziestu krów zysk spada do zera.

Zreasumujmy ekologię i ekonomię wspólnego pastwiska: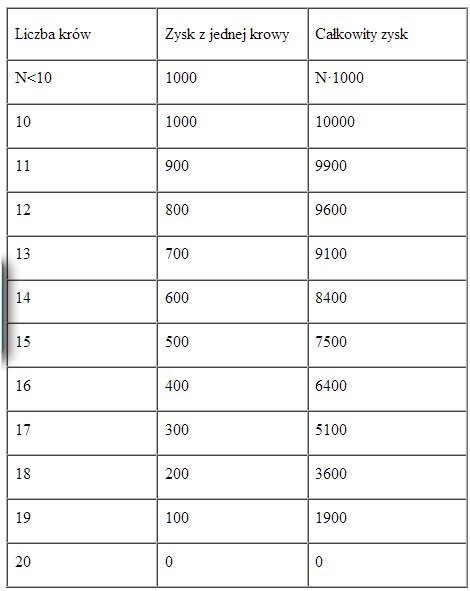

Początkowo kilku rolników wypasa na pastwisku po jednej krowie każdy. Roczny zysk każdego wynosi 1000$. Zysk całej wsi z pastwiska jest 1000$ razy liczba krów. Wprowadzanie dodatkowych krów zwiększa zyski inwestora i całej wsi, dopóki nie zostanie osiągnięta granica nasycenia — 10. Dla uproszczenia wywodu załóżmy dalej, co nie wpływa na ogólność wniosków, że te dziesięć krów pochodzi z dziesięciu zagród: każdy rolnik wypasa jedną. Każdy zarabia 1000$, wieś zarabia 10000$.

Co by się stało, gdyby jeden rolnik, kierując się własnym zyskiem, wprowadził na pastwisko dodatkową krowę. Wtedy każda krowa przynosiłaby po 900$, zysk wioski spadłby do 9900$, ale zysk egoisty wzrósłby do 1800$. Gdyby dalej ten sam lub inny egoista rozważał dodatkowe obciążenie pastwiska, tez by mu się to opłacało, gdyż każda z 12 krów przynosiłaby po 800$, cała wieś zarabiałaby 9600$, ale egoista (ten sam) miałby 2400$ zamiast 1800$ lub (inny) 1600$ zamiast dotychczasowych 900$. Odnotujmy tu pewną wartość dodaną: wszyscy tracą mniej, niż zyskuje egoista. W przypadku jedenastej krowy egoista zarabia 800$, społeczność traci 100$, w przypadku dwunastej społeczność traci jeszcze 300$, ale egoista zyskuje aż 600 lub 700$.

Pojedynczy egoista powinien się zatrzymać na piątej krowie: wtedy krów jest 14, każda daje po 600$, zatem jego krowy przynoszą mu 3000$. Gdyby obciążył pastwisko dodatkową krową, nic by nie zyskał, bo miałby teraz 6·500$, czyli tyle samo. Gdyby chciał posunąć się jeszcze dalej, miałby 7 krów z 16, ale zyskiwałby już tylko po 400$ na każdej, czyli łącznie 2800$, zatem mniej o 200$ niż w przypadku 5 lub 6 krów.

Jeśli jednak egoistów jest więcej, może dojść do „wyścigu szczurów". Pierwszy egoista mający 5 krów, woli mieć ich 6 czy 7, jeśliby się obawiał, że dodatkową krowę może wprowadzić ktoś inny: wszak wtedy ona sam traci na każdej z krów po 100$. Woli zatem obciążać pastwisko dalej, broniąc się przed ewentualną stratą.

Proces decyzyjny jest zawsze ten sam: wyłamanie się z koalicji, i dodatkowe obciążenie pastwiska jest dobrą indywidualną strategią. Gdy krów jest już 18, każda przynosi zysk 200$, wieś zarabia razem 3600$. Rolnik wprowadzający 19-tą krowę, jeśli wcześniej miał jedną, przynoszącą 200$ dochodu, teraz będzie miał dwie, dające po 100$, więc nic nie zyskuje — oprócz bezpieczeństwa, bo gdyby ktoś inny wprowadził następną, to on sam straciłby 100$. Gra zatrzymuje się na 19 krowach i łącznym zysku 1900$ zamiast początkowych 10000$.

Ginące pastwisko jest uważane za model konkurencji i kooperacji w obszarze dóbr niepodzielnych, takich jak środowisko, bezpieczeństwo, kultura itd.

GRY W PRAKTYCE

Licytacja o dolara pomiędzy USA a ZSRR — wyścig zbrojeń skończył się dezercją ZSRR, który nie odważył się dalej blefować, i zostawił Amerykę z problemami całego świata, w zamian za częściowe zwolnienie z zapłaty. W ekonomii i polityce licytacja o dolara zdarza się wtedy, kiedy decydent nie umie się wznieść poza kontekst lokalny i chwilowy, i dostrzec całości problemu. Działając profesjonalnie, podejmuje decyzje doraźnie i podręcznikowo poprawne, lecz ogólnie zgubne również dla siebie. Zabawnym, choć nie całkiem „czystym" przykładem jest podbijanie obietnic przeciwnika w kampanii wyborczej, które może prowadzić do zobowiązań dowolnie przekraczających możliwości państwa.

Często spotykanym i powszechnie rozumianym przykładem eskalacji modelowanej przez licytację o dolara jest banalna kłótnia o drobiazg, której strony podbijają bębenek ponad wszelką logikę według strategii:

- ciężko obraziłem partnera i — niezależnie od wyniku kłótni — koszty będą znaczne,

- ale nieznacznie zwiększając obrazę czy szantaż, niewiele podnoszę koszty, a przecież mogę wygrać.

Jedynym rozwiązaniem gwarantującym opłacalność licytacji o dolara jest zmowa: licytujący umawiają się, że jeden licytuje nisko, a drugi go nie przebija. Potem dzielą zysk. Tej strategii zagraża jednak wejście do gry kogoś spoza układu. Licznych przykładów zapobiegania temu dostarczają większe przetargi publiczne, wymyślnie ograniczające dostęp do licytacji.

Dylemat więźnia w praktyce bardzo często prowadzi do niekorzystnego dla więźnia wyboru. Często według scenariusza tego dylematu przebiegają kampanie wyborcze: niezależnie od trudności dowodowych, prawica oskarżająca lewicę o złodziejstwo (TN) wygrywa na tym, ale tylko do czasu, kiedy lewica zacznie rozgłaszać złodziejstwa prawicy (NT). Wtedy opinia publiczna, syntetyzując dwa komunikaty, zapamiętuje, że wszyscy politycy to złodzieje (TT) — polegając oczywiście nie na dowodach, których zwykle nie zna, lecz na oświadczeniach samych polityków. W dojrzałych i stabilnych systemach politycznych wytwarza się swoista zmowa milczenia wokół obyczajów i finansów polityków, zapobiegająca utracie dobrego imienia. Odpowiada to solidarności więźniów (NN).

W dawnej Europie przez stulecia normą były wspólne pastwiska. Ich historyczna klęska wyglądała inaczej, niż to przewiduje teoria gier, bowiem niektórzy wyszli poza reguły gry, eliminując konkurentów. Silniejsi zaczęli grodzić pastwiska, i odmawiać dostępu do nich wspólnocie. Gminne pastwiska zostały zawłaszczone przez jednostki, które siłą rzeczy zaczęły optymalizować swój zysk zgodnie z interesem ogółu użytkowników, czyli już indywidualnym, własnym. To rozwiązanie byłoby optymalne w ramach szerszej gry, przewidującej eliminację graczy.

See comments (2)..

Send text to e-mail address..

Print-out version..    MS Word

Marek Chlebuś Futurolog, członek Komitetu Prognoz PAN, autor kilku książek  Private site  Number of texts in service: 5  Show other texts of this author  Newest author's article: Przyszłość. Poradnik użytkownika