3. Ograniczenia systemów i ich charakterystyk

Najbardziej podstawową cechą dowolnej relacji podmiot-przedmiot jest jej ograniczoność, która wynika z nieustających zmian w przyrodzie. W naszych poprzednich pracach ideę ograniczeń wyprowadziliśmy z języków, w których istnieją ograniczone wyrazy i zdania oraz pojęcie 'czas życia', odnoszący się do wszystkich materialnych systemów. Ogólnie, koncept ograniczeń można uzasadnić w następujący sposób. Z fizyki wynika, że najbardziej ważnym ograniczeniem jest energia (E=Fq), wielkość której dla każdego rzeczywistego systemu musi być skończona oraz różna od zera (Eą0). Kiedy system zwiększa energię, to musi dokonać inwazję otoczenia, a kiedy system zmniejsza energię, to otoczenie dokonuje inwazję systemu. Inwazje te zależą od agresywności i wytrzymałości systemu i jego otoczenia. Ponieważ sztywność charakteryzuje również agresywność relacji podmiot-przedmiot, dlatego możemy powiedzieć: Jeżeli sztywność dF/dq i dq/dF dąży do zera (kiedy F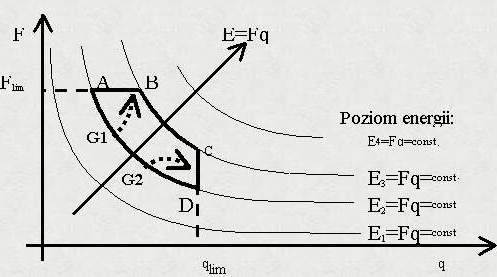0 i q lub q0 i F), to podmiot opisany przez 'F' staje się niezależny od przedmiotu 'q', i dlatego relacja podmiot-przedmiot {F,q} przestaje istnieć. Ponieważ wszystkie systemy posiadają cechę oporów, dlatego rzeczywista niezależność zachodzi dla F=F_bl >0 (dolna granica) i q=q_tl (górna granica) lub dla dolnej granicy q_bl >0 i górnej granicy F_tl. Dolną granicę można również nazwać koniecznością, a górną — możliwością. Kiedy dF/dq i dq/dF są odpowiednio duże efektywność relacji {F,q} staje się odpowiednio tak bardzo mała, że w pierwszym przypadku prowadzi system do bardzo dużej wewnętrznej i/lub zewnętrznej agresji, natomiast w drugim przypadku prowadzi do osłabienia systemu a następnie do jego zniszczenia przez otoczenie.

Rysunek 4. ilustruje koncepcja podstawowych ograniczeń relacji podmiot-przedmiot albo systemu obserwowanego albo doświadczonego przez człowieka. Przykładowo pole 'ABCD' reprezentuje ograniczenia każdego systemu. Jest ono wyznaczone przez odpowiednie poziomy energii 'E₂' i 'E₃', wielkość siły F_lim i zmian q_lim. W rzeczywistości granica tego pola 'ABCD' nie jest ostrą lecz rozmytą oraz bardziej nieregularną linią. W konsekwncji tego w wielu przypadkach występuje trudność w zauważeniu granic, szczególnie dla bardzo elastycznych (flexible) systemów jak na przykład w społecznych systemach i procesach. Ponadto, zależnie od systemu, jego otoczenia oraz rodzaju siły 'F' i zmian 'q', pole 'ABCD' może być różnie ulokowana w przestrzeni{(0-F),(0-q)}.

Załóżmy, że pewien system posiada:
— Pole sił z dwoma biegunami, gdzie jeden charakteryzuje się podmiotowymi, a drugi przedmiotowymi cechami (na przykład pole ekonomiczne posiadające biegun ludzi bogatych i drugi biegun ludzie biedni),
— 'F' oznacza wypadkową siłę oddziaływania między tymi biegunami powodującą pewne zmiany 'q',
— ograniczenia 'ABCD' jak zaznaczono na rys. 4.

Założenia te redukują analizowany system do prostej relacji podmiot-przedmiot, w której podmiot oddziałuje na przedmiot siłą 'F', wyniku tego zostają zrealizowane zmiany 'q', przy czym wartości 'F' i 'q' nie przekraczają pole 'ABCD'. Jeżeli podmiot działa ze zwiększającą się siłą zgodnie z zaznaczoną drogą 'E=Fq' (rys. 4.), to na tej drodze napotka ograniczenie 'BC', które jest zdeterminowane przez chwilową równowagę między systemem i jego otoczeniem. Przekroczenie tego ograniczenia jest naruszeniem równowagi oraz odzwierciedla inwazję i/albo systemu w stosunku do otoczenia.

Istniejąca silna motywacja wzrostu siły 'F' oraz brak odpowiedniej możliwości i/lub motywacji do inwazji otoczenia powoduje, że system może zwiększać siłę zgodnie z trajektorią 'G1' (rys. 4.). Ten wzrost powoduje wzrost sztywności dF/dq, gdyż podmiot zwiększa agresję w stosunku do przedmiotu, a który zwiększa opór w stosunku do tej siły i do zwiększania zmian 'q'. Sytuacja ta powoduje zwiększenie efektywności działania siły podmiotu. W celu szybkiego zwiększenia tej efektywności najczęściej system dokonuje agresji otoczenia. Jeżeli agresja otoczenia jest niemożliwa, to dalszy wzrost siły 'F' prowadzi w kierunku przekroczenia granicy 'AB' i osiąga punkt przełomowy (turning point). W punkcie tym w analizowanym systemie, siła 'F' traci swoje przedmiotowe cechy, a przedmiot staje się nowym podmiotem. Proces ten tym bardziej jest gwałtowny, im bardziej granica 'AB' będzie przekroczona.

W innym przypadku, kiedy siła 'F' rozwija się zgodnie z trajektorią 'G2' siła ta jest osłabiana, a zmiany zwiększają się. Ten proces osłabia system i pozwala na inwazję systemu przez otoczenie. W celu uniknięcia tego, zmiany 'q' nie mogą osiągnąć ograniczenie 'CD'. Kiedy zmiany osiągną limit 'q_lim', system ulega dezintegracji i zniszczeniu.

4. Cykliczne procesy zmian sztywności systemów

Ponieważ zmiany w przyrodzie są nieustające, dlatego systemy, w celu wydłużenia ich czasu egzystencji i/lub tożsamości muszą odpowiednio zmieniać wartości ich parametrów tak, aby nie przekraczały ograniczenia. Takie zmiany są możliwe tylko poprzez odpowiedni przemienne zwiększanie i zmniejszanie wartości parametrów. Taki proces nazywamy cyklicznym procesem zmian, który może być regularny lub nieregularny.

W odniesieniu do sztywności, cykliczne procesy zawierają zmiany, które odzwierciedlają zmiany między podmiotowymi i przedmiotowymi cechami elementów albo zmiany między dodatnimi i ujemnymi charakterystykami systemu. To może być zapisane jako {+dF/dq-dF/dq+dF/dq-dF/dq...} lub {dF/dqdq/dFdF/dqdq/dF...}. Natomiast w odniesieniu do energii, cykliczne procesy mają na celu konserwację energię (E=Fq=constant) przez system w odpowienio długim okresie czasu. Idealne procesy cykliczne konserwujące energię są harmonicznymi procesami, w których opór przeciwko przepływowi 'energii' we wszystkich kierunkach jest równy zeru. Zwykle są one modelowane przy pomocy następującego równania różniczkowego sztywności Ld2f(t)/dt2+Rdf(t)/dt+f(t)=f₀sin(wt+f), gdzie opór R=0, i wymuszająca funkcja f₀sin(wt+f)=0.

Szczególnie liczna klasa ciągłych cyklicznych procesów, która również zawiera rozwiązania poprzednio wymienionego równania różniczkowego drugiego rzędu, reprezentuje zbiór funkcji wyznaczonych przez wyrażenie f(t)=f₀f₁(t)sin[w(t)t+f]. W tym zbiorze mogą być procesy cykliczne harmoniczne, zbieżne i rozbieżne w zależności od funkcji f₁(t), a ich cykle mogą być regularne i nieregularne w zależności od w(t). Lecz podobnie do monotonicznych procesów, wszystkie wartości parametrów tych procesów cyklicznych sa odpowiednio ograniczone poprzez górny i dolny limit, jak na przykład amplitudy, częstotliwości i okresy cyklów. W rzeczywistości odpowiednio długi okres cyklicznego procesu jest dla wielu elementów procesem monotonicznym, natomiast odpowiednio krótki okres cyklów zmniejsza stabilność elementów odpowiednio związanych z tym procesem. Jak już wcześniej wspomnieliśmy, zaprezentowana powyżej metoda modelowania cyklicznych procesów bazująca na czasie tworzy poważny problem, gdyż usuwa albo ukrywa relacje podmiotowo-przedmiotowe. Dlatego często między innymi przyczynia się do kształtowania opinii, że w przyrodzie nie istnieje przyczynowość oraz ze względu na silny wpływ języka na ludzki umysł powoduje to, że w naukach zawsze szuka się relacji albo korelacji podmiot-przedmiot. Systemy, które najczęściej funkcjonują w sposób cykliczny, to różnego rodzaju urządzenia techniczne a w tym silniki.

W przyrodzie, wszystkie długo istniejące zjawiska funkcjonują na bazie cyklicznych procesów. W tym również dużo systemów i procesów społecznych funkcjonuje cyklicznie, ponieważ są one częścią względnie długo trwającego zjawiska życia na Ziemi. Właśnie w funkcjonowaniu społeczeństw i społecznych procesów bardzo wyraźnie zauważamy cykliczność różnych. Cykliczność jest związana z uczuciami motywacji, czego szczególnym przykładem jest powtarzalność różnych idei w modzie. Innym interesującym zjawiskiem, którego istnienie wynika z cykliczności jest zjawisko absurdu przesady szczególnie celowo wykorzystywane w dowcipach. Zgodnie z naszymi badaniami, można powiedzieć, że społeczne cykliczne procesy tworzą podstawowe ramy dla wszystkich systemów społecznych, i one w wielkim stopniu determinują trwanie egzystencji i tożsamości społeczeństw, społecznych systemów, organizacji i indywidualnych ludzi. Ponieważ przyroda charakteryzuje się ogromną różnorodnością, dlatego istnieje ogromna liczba różnych cyklicznych procesów, i dlatego istnieje bardzo wiele różnych klas funkcji cyklicznych zarówno empirycznych jak i teoretycznych.

Najważniejszym problemem jaki stoi przed współczesnymi społeczeństwami jest skrajnie silna motywacja, jak i aktywność utrzymania monotonicznego wzrostu populacji ludzi na świecie i ekonomii. Ponieważ jest to sprzeczne z naturalną zasadą cykliczności realizowaną w sposób ewolucyjny przez długotrwałe procesy, dlatego zachodzą i będą się nasilać gwałtowne spontaniczne i zorganizowane procesy mające na celu utrzymania cykliczności w naturalnym otoczeniu, ekonomii i innych społecznych systemach oraz procesach. Dlatego istnieje silne zagrożenie, że taki dalszy rozwój może przekroczyć niebezpieczne ograniczenie inicjując turbulentny społeczny konflikt wśród ludzi oraz między ludźmi a przyrodą.

Pozytywnym społecznym przykładem funkcjonowania stopniowych cyklicznych procesów jest polityczna demokracja, która powoduje regularne cykliczne zmiany rządów. Najważniejszymi cechami demokracji są cykliczne zmiany politycznych dysproporcji w społeczeństwie oraz ograniczenia tych dysproporcji w szczególnym przypadku poprzez elekcję. Jeżeli elekcja funkcjonuje efektywnie, to ogranicza ona siłę rządu i polityków (górne ograniczenie), a zwiększa siłę zwykłych ludzi (dolne ograniczenie). Ponadto, polityczna siła polityków i zwykłych ludzi zmienia się w czasie wyborów, po oraz przed wyborami. W myśl tej prostej koncepcji, możemy powiedzieć, że demokracja albo demokratyczny proces jest procesem, w którym dysproporcje między silnymi i słabymi elementami społecznymi zmieniają się w sposób cykliczny i ewolucyjny. Takie zmiany są możliwe, jeżeli dysproporcje te nie przekroczą pewnego górny i dolny limitu. W związku z tym, ekonomiczną demokrację determinują cykliczne zmiany dysproporcji ekonomicznych między warstwami bogatymi i biednymi, przy czym dysproporcje te nie mogą być przesadnie duże lub małe (Turkiewicz DB and Turkiewicz K, 2003).

Współcześnie, w wyniku globalizacji, ekonomiczne procesy tworzą najsilniejsze pole siły społecznej, i dlatego posiadają największy wpływ na pozostałe pola i procesy. Ponieważ główną ideą współczesnej ekonomii jest stały monotoniczny wzrost jej sił i wyeliminowanie cykliczności, dlatego obecna ekonomia i tak zwany Zachodni świat są niedemokratyczne. Podobnie proces wzrostu populacji ludzi na świecie jest również niedemokratyczny. Dlatego efektywność i istnienie politycznej demokracji oraz ewolucyjne zmiany w społeczeństwach i naturalnym otoczeniu są w poważnym zagrożeniu od wymienionych dwóch bardzo silnych procesów.

5. Zakończenie

Zaprezentowana analiza lingwistycznej relacji podmiot-przedmiot bazująca na sformalizowanych modelach wykorzystujących ciągłe funkcje pokazuje, że ma ona bardzo silny wpływ na wszystkie nauki. Wpływ ten wynika z podstawowego aspektu języka, bez którego nie jest możliwa identyfikacja i zrozumienie dowolnego zjawiska i bez którego nauki nie mogłyby rozwinąć się od obecnej postaci. Ponieważ relacja podmiot-przedmiot jest organicznie i na stałe włączona do ludzkiego umysłu, jest ona używana w sposób automatyczny i podświadomy. Dlatego, pomimo braku świadomości tej relacji, jest ona zawsze podstawowym elementem każdej teorii naukowej oraz ona najbardziej łączy zróżnicowane dziedziny nauki. Oprócz energii również bardzo ważną cechą relacji podmiot-przedmiot sztywność, która pozwala analizować podstawowe zachowanie się wszystkich typów systemów. Jest ona już odpowiednio rozwinięta przez nauki dla pewnych systemów, może ona być rozwinięta lub odnowiona dla innych.

Podsumowując analizę społecznych procesów bazującą na fizykalnym modelowaniu relacji podmiot-przedmiot, możemy powiedzieć, że cykliczne procesy tworzą najważniejszą ramę albo podstawę dla względnie długo-trwałych społecznych procesów i systemów. Monotoniczne procesy przeważnie są ich elementami, są sterowane w adaptacyjny sposób, i dlatego pomijają analizy przyszłości systemów i ich otoczeń. Dlatego taki typ sterowania ułatwia przesadny monotoniczny wzrost systemów, co prowadzi do gwałtownych konfliktów z długo-trwałymi cyklicznymi procesami. Z drugiej strony, antycypacyjny sposób sterowania, który analizuje ewolucyjną cykliczną przyszłość systemów pozwala na silne ograniczenie gwałtownych konfliktów, i dlatego przyczynia się do demokracji wszystkich społecznych procesów.

Literatura
Liboff R.L. (2003). Introductory Quantum Mechanics. 4^th Edition, Addison Wesley, New York.
Sussman G.J., Wisdom J. and Mayer M.E. (2001). Structure and Interpretation of Classical Mechanics. The MIT Press, Cambridge.
Turkiewicz K.,Turkiewicz D.B. (2002). "The Role of the Structure of the Conditional Sentence in Sciences", The XV^th ISA World Congress of Sociology Brisbane, Australia, July 7-13.
Turkiewicz D.B., Turkiewicz K. (2003). „Holistic Analysis of the Physical Nature of Democracy and Terrorism", in InterSymp 2003, The 15^th International Conference on System Research, Informatics and Cybernetics, Baden-Baden, Germany, July 28-August 2.
Wittgenstein L. J. (1961). Tractatus Logico Philosophicus. Routledge and Kegan Paul, London.

Ninijesza praca pod tytułem 'Formalised Synthetic Modelling of Subject — Object Relations' została opublikowana w „CASYS, International Journal of Computing Anticipatory Systems" wydawanym przez D.M.Dubois, w maju 2004.

Po przeczytaniu tego tekstu, czytelnicy często wybierają też: Zrozumieć organizację sformalizowaną Wobec nauki. Analiza stanowiska metodologicznego Edmunda Husserla

Comment on this article..

Send text to e-mail address..

Print-out version..    PDF    MS Word